Предмет: Алгебра,
автор: Karaseek
Даю много баллов!
Составьте уравнение касательной к графику функции
y = 2x - 7 : 2x - 5, в точке с абсциссой  = 3
= 3
Приложения:
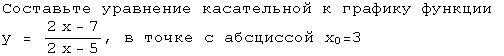
Ответы
Автор ответа:
0
Производная равна: y' = (2*(2x - 5) - 2*(2x - 7)/((2x - 5)²) = 4/((2x - 5)²).
Значение производной в точке х = 3 равно 4/(2*3-5) = 4.
Значение функции в точке х = 3 равно (2*3-5)/(2*3-7) = -1.
Ответ: y(кас) = 4*(х -3) - 1 = 4х - 12 - 1 = 4х - 13.
Автор ответа:
1
Похожие вопросы
Предмет: Литература,
автор: 052007katya
Предмет: Алгебра,
автор: hfdguuyfdry
Предмет: Математика,
автор: ira8870
Предмет: Математика,
автор: slayd1
Предмет: Химия,
автор: Sluger