Предмет: Геометрия,
автор: qwertywat
40 баллов за одну задачу на планиметрию!
Площадь прямоугольного треугольника разделена пополам прямой, перпендикулярной гипотенузе. Найдите расстояние между этой прямой и вершиной меньшего из острых углов,если больший катет равен 20 см.
Помогите, пожалуйста. Составьте чертёж и объясните, как решить.
Ответы
Автор ответа:
4
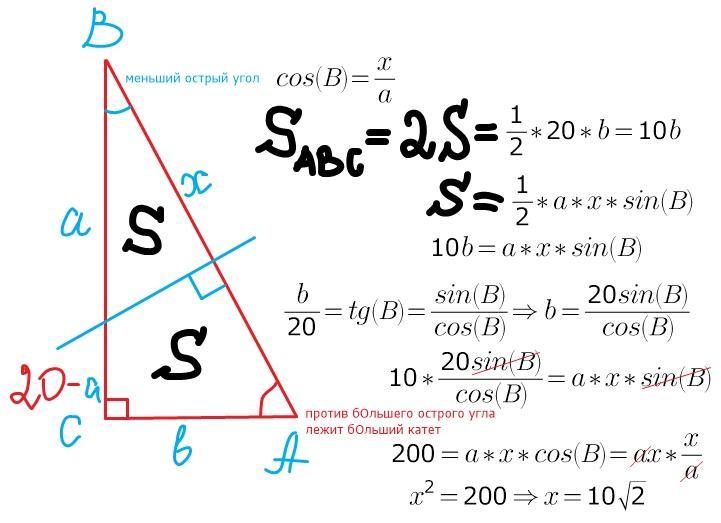
проще всего, наверное, через площадь решать...
площадь прямоугольного треугольника = половине произведения катетов...
площадь любого треугольника (в том числе и прямоугольного) = половине произведения двух сторон на синус угла между ними...
расстояние от точки до прямой--это перпендикуляр))
Приложения:
Автор ответа:
4
Вариант решения.
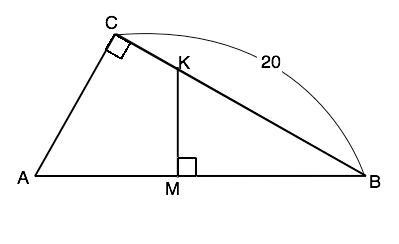
Пусть в треугольнике АВС ∠С=90°, В - вершина меньшего острого угла, а КМ – перпендикуляр к гипотенузе. Расстояние от точки до прямой равно длине перпендикуляра между ними. Искомый отрезок - ВМ.
Δ АВС подобен Δ КВМ по общему острому углу СВА.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
По условию Ѕ(АСВ):Ѕ(КВМ)=2, и это отношение равно k² . ⇒ k=√2, следовательно, ВС:BM=√2 ⇒ MB=BC:√2=20:√2=10√2 см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Grechka8
Предмет: Кыргыз тили,
автор: jsjjwnenejjej
Предмет: Қазақ тiлi,
автор: aminakonys2011
Предмет: Математика,
автор: mail20045
Предмет: Алгебра,
автор: Salihovaa