Диагональ равнобедренной трапеции делит высоту, проведенную из вершины тупого угла, на отрезки длиной 10 см и 8 см.
Найдите площадь трапеции, если ее меньшее основание равно боковой стороне трапеции.
Ответы
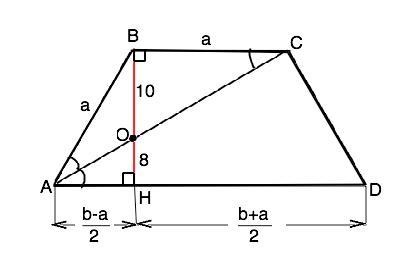
Пусть в трапеции АВСD (BC||AD) диагональ пересекает высоту ВН в точке О, ВО=10 см, ОН=8 см. Примем ВС=AB=CD=а, АD=b.
Диагональ АС и высота ВС при пересечении образуют с частью оснований прямоугольные треугольники, подобные по равным острым углам (при О и накрестлежащим ВСА=СAD). Коэффициент подобия k=ОН:ОВ=8:10=0,8. Поэтому АН=0,8а.
Из ∆ ВАН по т.Пифагора АВ²-АН²=ВН²⇒ а²-0,64а²=0,36а²⇒а=30 см. ⇒ АН=0,8•30=24 см
В равнобедренной трапеции высота из тупого угла делит основание, к которому проведена, на отрезки, меньший из которых равен полуразности оснований, а больший - их полусумме. ⇒
АН=(b-a)/2, HD=(b+a)/2. Из найденного выше (b-a):2=24,⇒ b-30=48 ⇒b=48+30=78.
Площадь трапеции равна произведению высоты на полусумму оснований. Высота ВН=ВО+ОН=18 см, полусумма оснований (a+b):2=(30+78):2=54 см. S(ABCD)=18•54=972 см²
Пусть АВСД - данная трапеция. ВС║АД, Диагональ АС пересекается с высотой трапеции ВТ в точке О, ВС=АВ=СД=х, Проведем еще одну высоту СF=FТ=х, FД=АТ=у, ВО=10, ТО=8, треуг. СFА и ОТА подобны по двум углам, по прямому и общему углу А, составим пропорцию, СF/ОТ=FА/ТА, или у/8=(х+у)/18, (18-8)*у=8х, откуда х=0, 8у, 18²+у²=х², 18²=х²-0,64х², 0,36х²=18², откуда модуль икс равен 30, т.к. это сторона, то положит. х=30, тогда у=0,8*30=24, а площадь равна
((2х+2у)*18/2)=(30+24)*18=972/см²/
Ответ 972 см²