Предмет: Математика,
автор: YkharitonovaM
Найдите производную
Пожалуйста
Приложения:
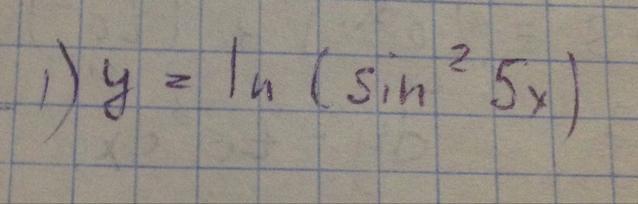
Ответы
Автор ответа:
1
Ответ: 10ctg5x
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: aliii36
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: prohorolesa
Предмет: Химия,
автор: yanatihonova0
Предмет: Математика,
автор: Аноним