Предмет: Геометрия,
автор: 123KaTuShA123
!Даю 39 баллов. !
В прямоугольном треугольнике ABC( с прямым углом С) заданы катеты АС=6, вс=9. Найдите медиану CM.
Ответы
Автор ответа:
0
пусть ас = b
bc = a
ab= c
тогда cm
по th.пифагора
получим
Приложения:
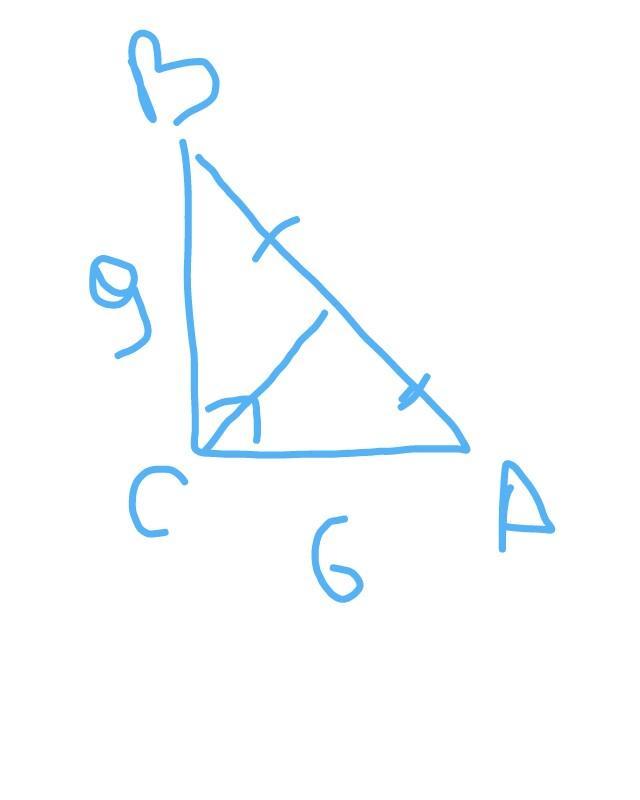
Автор ответа:
1
По катетам находим гипотенузу по Пифагору, т.е. √(9²+6²)=√117
А медиана, проведенная к гипотенузе равна ее половине, т.к. середина гипотенузы является центром описанной около треугольника окружности, значит, отстоит от всех вершин на одно и то же расстояние. Значит, медиана равна √117/2
Похожие вопросы
Предмет: Химия,
автор: sasukeeeee13
Предмет: Математика,
автор: svitlanasmilianets
Предмет: Литература,
автор: pn911824
Предмет: Математика,
автор: Викуля512
Предмет: Геометрия,
автор: NikKravts