Предмет: Алгебра,
автор: jazzavto
Помогите решить пример, чтобы получился такой ответ(картинка 2), у меня получился через арксинус.
Приложения:
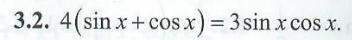

Ответы
Автор ответа:
1
P.S. Если в уравнении одновременно присутствуют сумма sinx и cosx , а также их произведение, то метод решения - замена t=sinx+cosx.
Похожие вопросы
Предмет: Русский язык,
автор: ruslan2121200566
Предмет: Психология,
автор: kimgo4ka1111
Предмет: Литература,
автор: 764756tab
Предмет: Литература,
автор: oleat04
Предмет: Химия,
автор: М092001