Предмет: Алгебра,
автор: ClarisVerbis
Задание представлено в закрепе ниже.
Приложения:
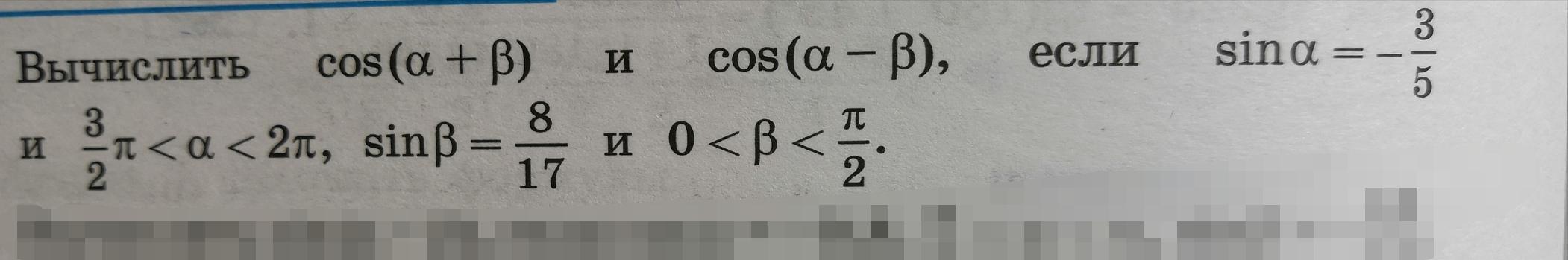
Ответы
Автор ответа:
1
α - угол четвёртой четверти, значит : Cosα > 0
β - угол первой четверти , значит : Cosβ > 0
Похожие вопросы
Предмет: Математика,
автор: Abdulvadud30morsings
Предмет: История,
автор: shoxruxnazarov7755
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: zzzzzzzzzz03