Question

Периметр параллелограмма равен 360, а его острый угол равен 60°. Найдите стороны параллелограмма, Если известно, что его меньшая диагональ делит его углы в отношении 3:1

Answer 1

Так как в параллелограмме противоположные углы равны, а сумма внутренних углов равна 360°, то вторая пара углов:

                (360 - 2·60) : 2 = 120°

Так как меньшая диагональ делит бо'льшие углы параллелограмма, то:

                х + 3х = 120

                   х = 30°           3х = 90°

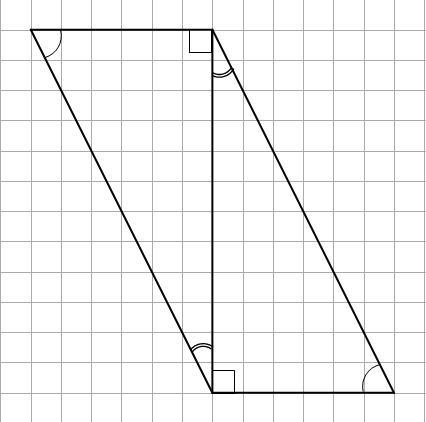
Таким образом, параллелограмм состоит из двух прямоугольных треугольников с общим катетом, в качестве меньшей диагонали.

Так как меньший угол треугольника 30°, то катет, лежащий напротив этого угла равен половине гипотенузы. Обозначим их:  х и 2х, соответственно.  

Тогда, учитывая, что периметр параллелограмма равен 360 (ед.):

      2х + 4х = 360

        х = 60 (ед.)     2х = 120 (ед.)

Ответ: 60 ед.; 60 ед.; 120 ед.; 120 ед.