Исследовать функцию с помощью производных и построить график . Пожалуйста, помогите!!!

Ответы
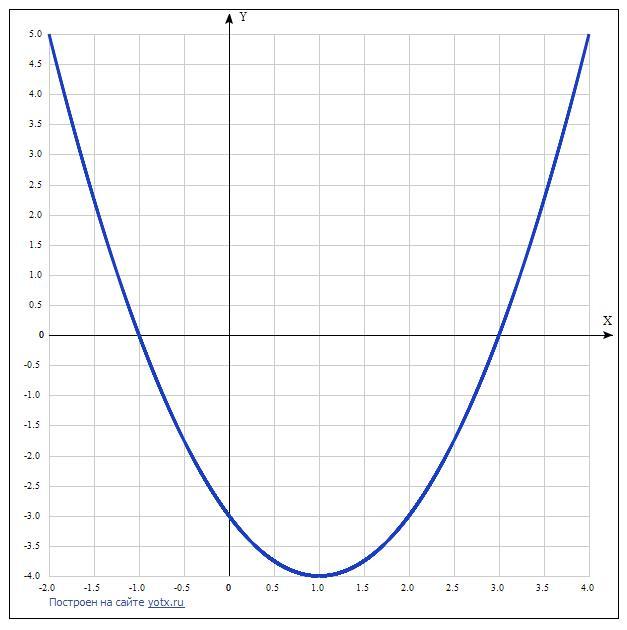
Полное исследование функции у = х² - 2х - 3 по схеме:
1. Область определения функции - ограничений нет, х ∈ Z.
2. Непрерывность функции - да, вертикальные асимптоты - нет.
3. Точки пересечения функции с осями координат.
- с осью Оу при х = 0. у = 0² - 2*0 - 3 = -3.
- с осью Ох при у = 0.
Надо решить квадратное уравнение х² - 2х - 3 = 0. Д = 4 +12 = 16.
х1 = (2 + 4)/2 = 3, х2 = (2 - 4)/2 = -1.
4. Четность, нечетность. f(-x) = x² + 2x - 3 ≠ f(x). Функция общего вида.
5. Периодичность - нет.
6. Промежутки возрастания, убывания, экстремумы функции.
Производная равна y' = 2x - 2 = 2(x - 1). Приравняем нулю и находим одну критическую току х = 1. Для определения характера её находим знаки производной левее и правее этой точки.
х = 0 1 2
y' = -2 0 2.
Значит х = 1 это точка минимума функции (переход от - к +).
Значение функции в этой точке у = 1 - 2 - 3 = -4.
На промежутке (-∞; 1) функция убывает (y' < 0), на промежутке (1; +∞) функция возрастает (y' > 0).
7. Промежутки выпуклости, вогнутости, точки перегиба.
Вторая производная y'' = 2. Она не равна 0, значит точки перегиба нет. Вторая производная положительна, значит, функция вогнута.
8. Наклонные асимптоты - нет.
9. Построение графика по точкам.
x y
-2.0 5
-1.5 2.25
-1.0 0
-0.5 -1.75
0 -3
0.5 -3.75
1.0 -4
1.5 -3.75
2.0 -3
2.5 -1.75
3.0 0
3.5 2.25
4.0 5.