Предмет: Математика,
автор: marmelade2908
ПОЖАЛУЙСТА!
Выразите | sinx-cosx | через a, если sinx+cosx= a
Ответы
Автор ответа:
0
sinХ + cosХ = a;
1 решение.
Возведем условие в квадрат:
sin^2(x) + 2sin(x)cos(x) + cos^2(a) = a.
Используя основное тригонометрическое тождество, получим:
2sin(x)cos(x) = a - 1.
Возводим в квадрат исходное выражение:
(|sin(x) - cos(x)|)^2 = sin^2(x) - 2sin(x)cos(x) + cos^2(x) = 1 - 2sin(x)cos(x) = 1 - (a - 1) = 2 - a.
Тогда:
|sin(x) - cos(x)| = √(2 - a).
2 решение.
sinx+cosx=a
sinx+sin(π/2-x)=2sinπ/4cos(x-π/4)=√2cos(x-π/4)=a
cos(x-π/4)=a/√2
sin(x-π/4)=√(1-cos²(x-π/4))²=√(1-a²/2)=√(2-a²)/√2
sinx-cosx=sinx-sinx(π/2-x)=2sin(x-π/4)cosπ/4=√2sin(x-π/4)
|sinx-cosx|=|√2sin(x-π/4)|=√2*√(2-a²)/√2=√(2-a²)
3 решение.
фото...
Приложения:
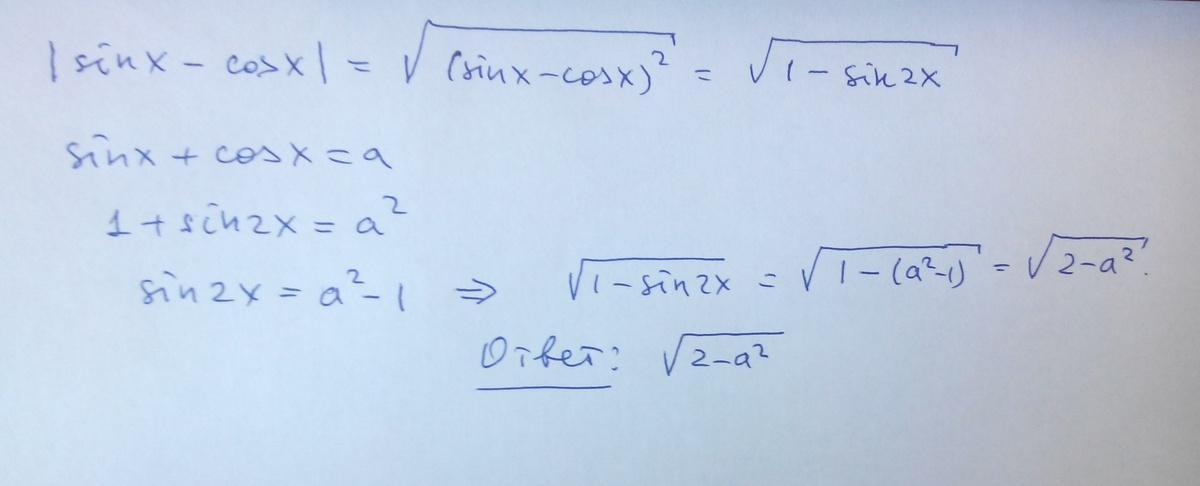
Похожие вопросы
Предмет: Биология,
автор: victoriakravchenko10
Предмет: Українська література,
автор: karinazabolotna37
Предмет: Биология,
автор: mrfreez59
Предмет: Обществознание,
автор: LoliPeen
Предмет: Физика,
автор: DanielDavydov