Предмет: Алгебра,
автор: denandreev2001
Решите логарифмическое неравенство
(10 класс; уровень сложности: средний)
Смотрите фотографию (Задание 2)
Оформить письменно!
x^lg(x)<=100x
Приложения:
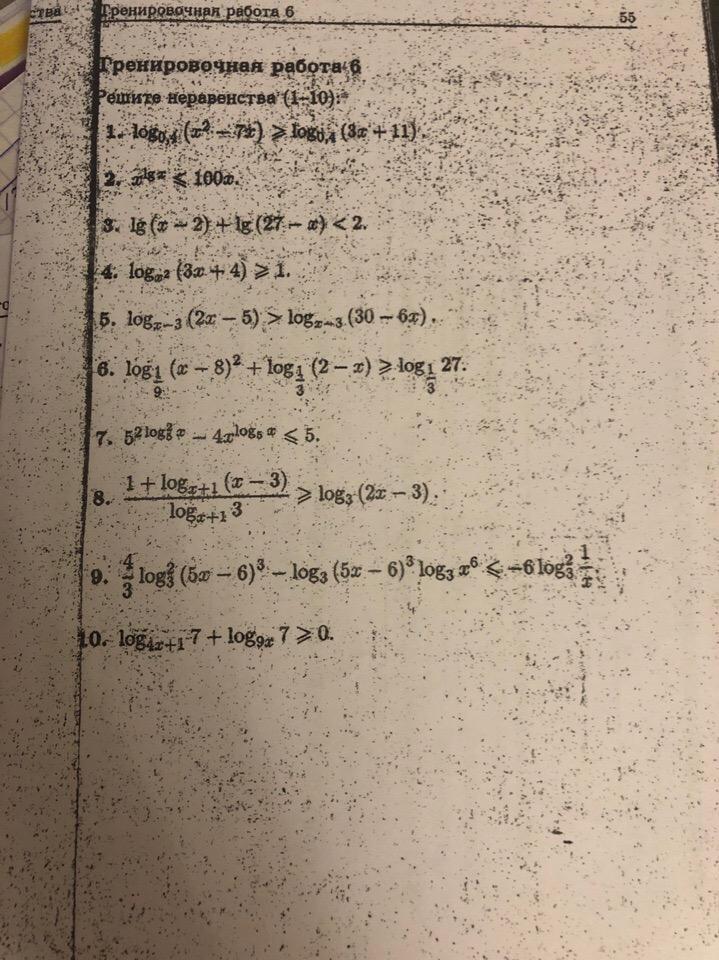
Ответы
Автор ответа:
3
ОДЗ: x > 0
следовательно, обе части неравенства--это положительные числа)
можно прологарифмировать обе части неравенства по основанию 10:
lg(x) * lg(x) ≤ lg(100) + lg(x)
заменой t=lg(x) неравенство сведется к квадратичному...
t² - t - 2 ≤ 0 по т.Виета корни t₁=2 и t₂=-1
и решение "между корнями" (парабола, ветви вверх...)
-1 ≤ lg(x) ≤ 2
lg(0.1) ≤ lg(x) ≤ lg(100) основание логарифма 10>1 ⇒ знаки не меняются...
0.1 ≤ x ≤ 100
Похожие вопросы
Предмет: Алгебра,
автор: xiaomi88738
Предмет: Информатика,
автор: dmetromt
Предмет: Геометрия,
автор: antoninkapetrovna
Предмет: Алгебра,
автор: Olesya9899
Предмет: Физика,
автор: essen11111
Я просто задавал вопрос по решению этих неравенств, так никто и не сумел решить
Могу отправить ссылку вам на эти задания
Там я даю по 30; 45 баллов...