Предмет: Математика,
автор: Diana5D
Исследовать ряд на сходимость
Приложения:
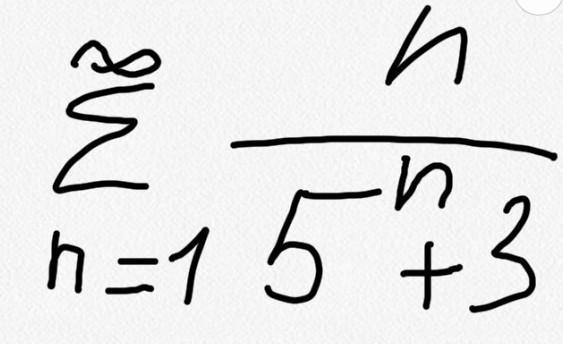
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: muminaqobiljonova201
Предмет: Українська література,
автор: saymonmyr
Предмет: Алгебра,
автор: Katr1n008
Предмет: Химия,
автор: ustimenkoelena
Предмет: Биология,
автор: sani567