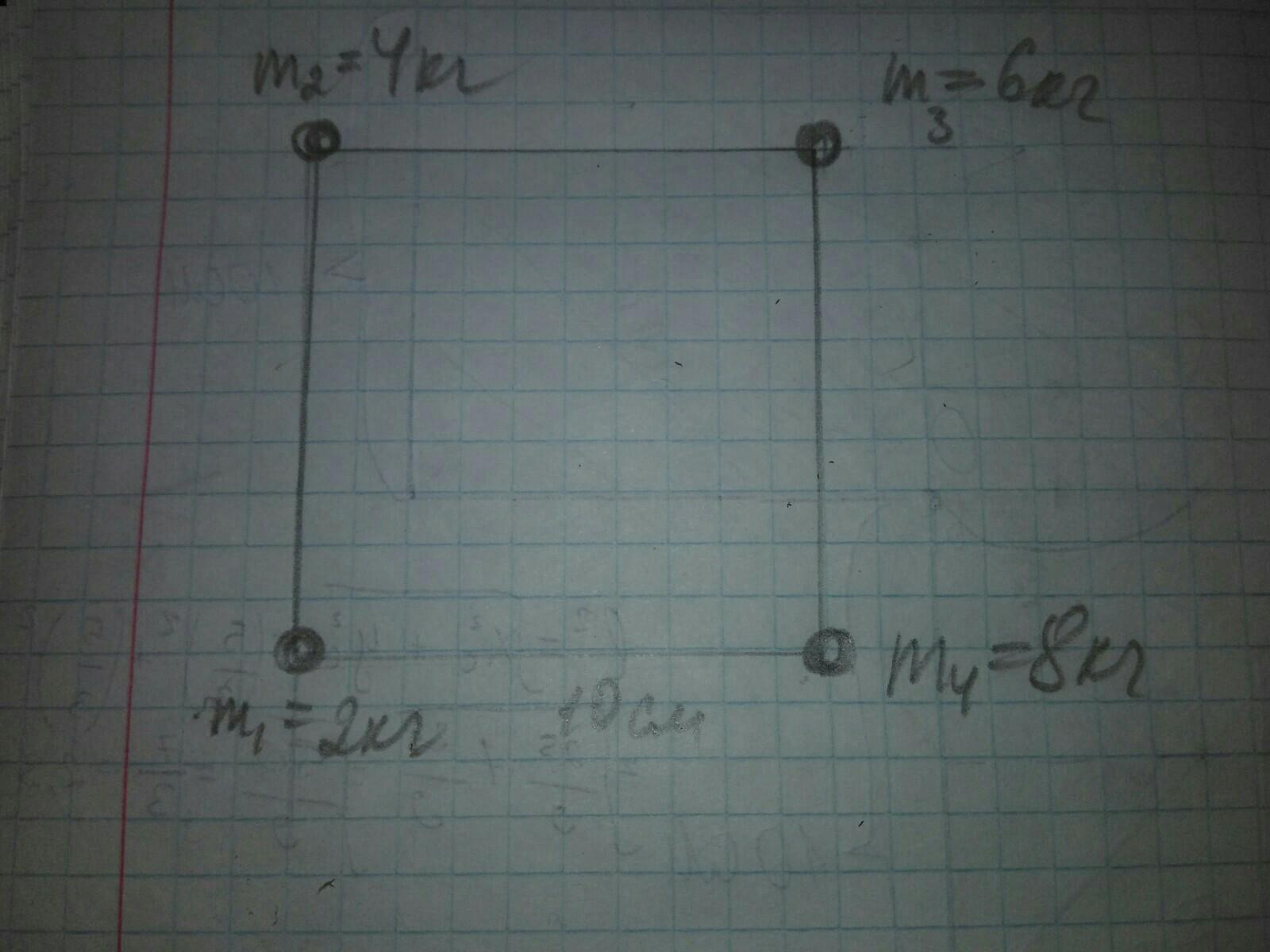
Найдите центр тяжести однородной плоской пластины, показанной на рисунке, если:
m (1) = 2 кг; m (2) = 4 кг;
m (3) = 6 кг; m (4) = 8 кг.
Стороны равны 10 см.
Ответы
Сумма масс M = m1+m2+m3+m4 = 2+4+6+8 = 20 кг
a = 10 см
Xc = (m3+m4)*a / M = (6+8)*10 / 20 = 7 см
Yc = (m2+m3)*a / M = (4+6)*10 / 20 = 5 см
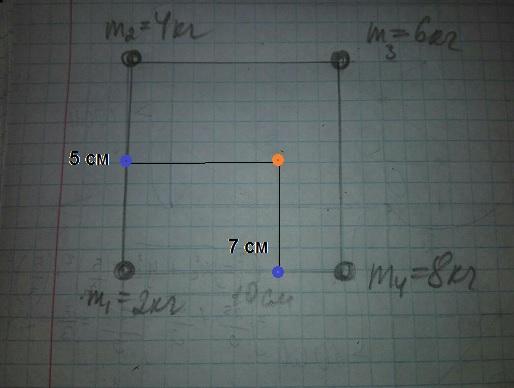
Данную пластину можно рассматривать как систему двух рычагов:
1) Рычаг, расположенный вдоль оси X, общая длина которого равна a, на левом плече расположен груз массой m1+m2, а на правом груз массой m3+m4. Координату равновесия этого рычага Xc найдём из условия равновесия рычага:
(m1 + m2)×Xc = (m3+m4)×(a-Xc)
Подставив значения масс и стороны а, получим уравнение:
6×Xc = 14×(10-Xc)
6Xc = 140 - 14Xc
20Xc = 140
Xc = 140/20 = 7
Итак, координата Xc = 7 см
2) Рычаг, расположенный вдоль оси Y, общая длина которого равна a, на нижнем плече расположен груз массой m1+m4, а на верхнем груз массой m2+m3. Координату равновесия этого рычага Yc найдём из условия равновесия рычага:
(m1 + m4)×Yc = (m2+m3)×(a-Yc)
Подставив значения масс и стороны а, получим уравнение:
10×Yc = 10×(10-Xc)
10Yc = 100 - 10Yc
20Yc = 100
Yc = 100/20 = 5
Итак, координата Yc = 5 см
Ответ: координаты центра тяжести пластины равны Xc = 7 см, Yc = 5 см