Предмет: Математика,
автор: luninvladislav2014
СРОЧНО Решить задачу Коши
m=1
n=2
Приложения:
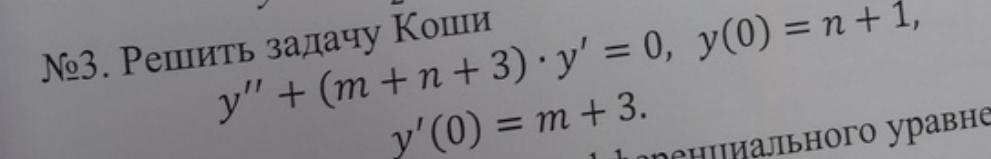
Ответы
Автор ответа:
0
y"+6y'=0, y(0)=3, y'(0)=4
Линейное однородное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение :
k^2+6k=0
k(k+6)=0
k=0 или k=-6 -- различные действительные корни, следовательно

Определим постоянные с1 и с2, используя начальные условия.
Найдем у'(х):



Таким образом, решением задачи Коши будет являться функция

Линейное однородное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение :
k^2+6k=0
k(k+6)=0
k=0 или k=-6 -- различные действительные корни, следовательно
Определим постоянные с1 и с2, используя начальные условия.
Найдем у'(х):
Таким образом, решением задачи Коши будет являться функция
Похожие вопросы
Предмет: Английский язык,
автор: z5das
Предмет: Физика,
автор: Аноним
Предмет: Русский язык,
автор: kvitkomaria89
Предмет: Математика,
автор: felofery
Предмет: Химия,
автор: Аноним