Предмет: Алгебра,
автор: gooding1904
Срочно!!!
Положительные числа x и y таковы, что x^2+(y^2)/9=6. Найдите наибольшее возможное значение выражения xy.
ТатМих:
На 9 делится только (y^2)? или вся сумма?
только (y^2)
Ответы
Автор ответа:
18
Если максимально, то и
тоже максимально.
Выражаем из равенства и подставляем в выражение:
Получившееся выражение – квадратичная функция относительно . Известно, что максимум такой функции достигается в вершине, в данном случае – при
Тогда ,
'
Этим значениям x и y соответствует значение произведения
Ответ. 9
Ты лучшая
Автор ответа:
18
ответ 9
просто свой способ )
Приложения:
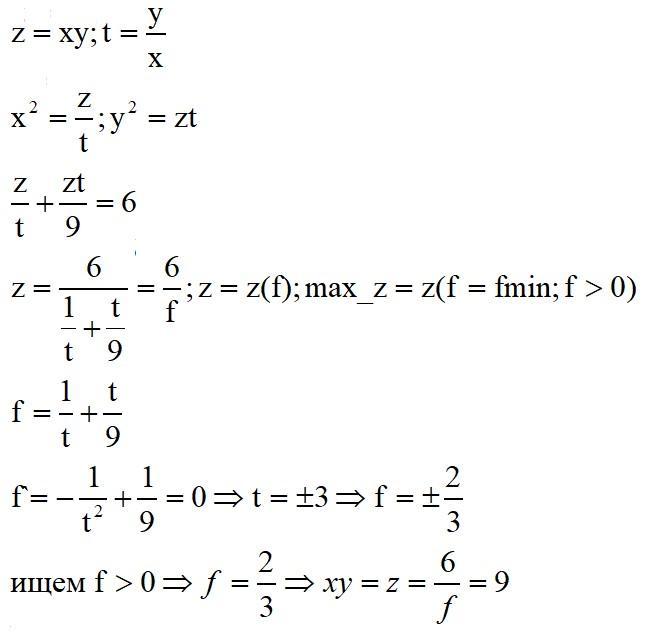
Похожие вопросы
Предмет: Английский язык,
автор: henkanderson136
Предмет: Физика,
автор: gfd39371
Предмет: Алгебра,
автор: artemliontev06
Предмет: Математика,
автор: WindowsXpServicePack
Предмет: Математика,
автор: Аноним