Question

площадь прямоугольного треугольника равна 32 корень из 3 один из острых углов равен 30 Найдите длину гипотенузы​

Answer 1

Дано :

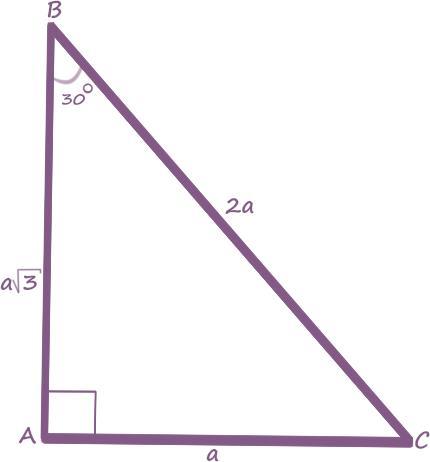
ΔАВС - прямоугольный (∠А = 90°).

S(ΔABC) = 32√3 (ед²).

∠В = 30°.

Найти :

ВС = ?

Решение :

Пусть ВС = 2а.

• Против угла в 30° лежит катет, равный половине гипотенузы.

Следовательно -

АС = ВС/2 = 2а/2 = a.

$Cos(\angle B) = \frac{AB}{2a}$ (по определению косинуса острого угла прямоугольного треугольника)

$Cos(30^{\circ} ) = \frac{AB}{2a} \\\\\ \frac{\sqrt{3} }{2} = \frac{AB}{2a}\\\\2a\sqrt{3} = 2AB\\\\\boxed{AB = a\sqrt{3}}$

• Площадь прямоугольного треугольника равна половине произведения его катетов.

Следовательно -

S(ΔABC) = 0,5*АВ*АС = 0,5*(а√3)*а = 0,5*а²√3 = 32√3 (ед²)

0,5*а²√3 = 32√3

а²√3 = 64√3

а² = 64

а = 8.

ВС = 2а = 2*8 = 16.

Ответ :

16.