Предмет: Алгебра,
автор: ClarisVerbis
Задание прикреплено ниже.
Приложения:
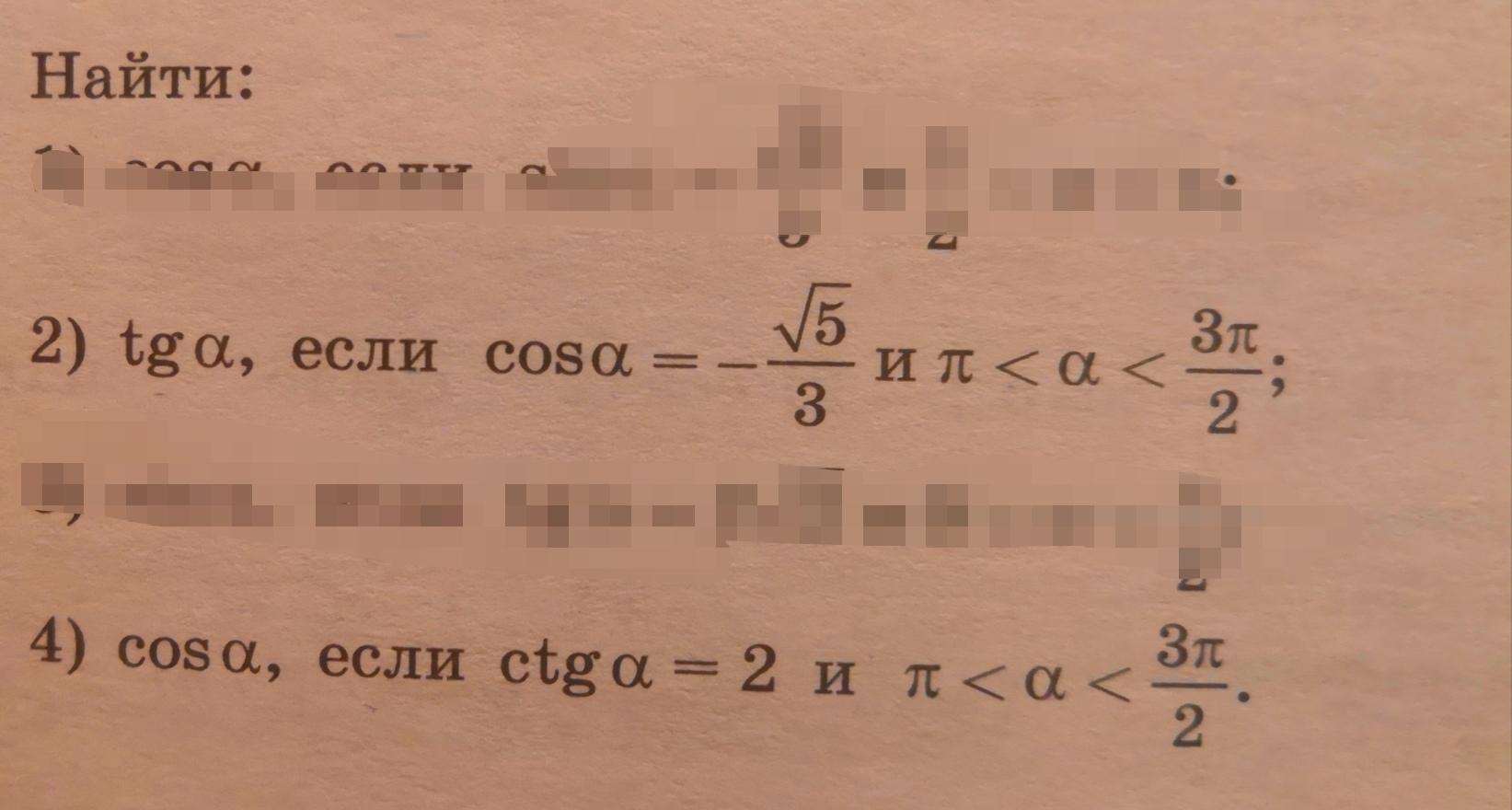
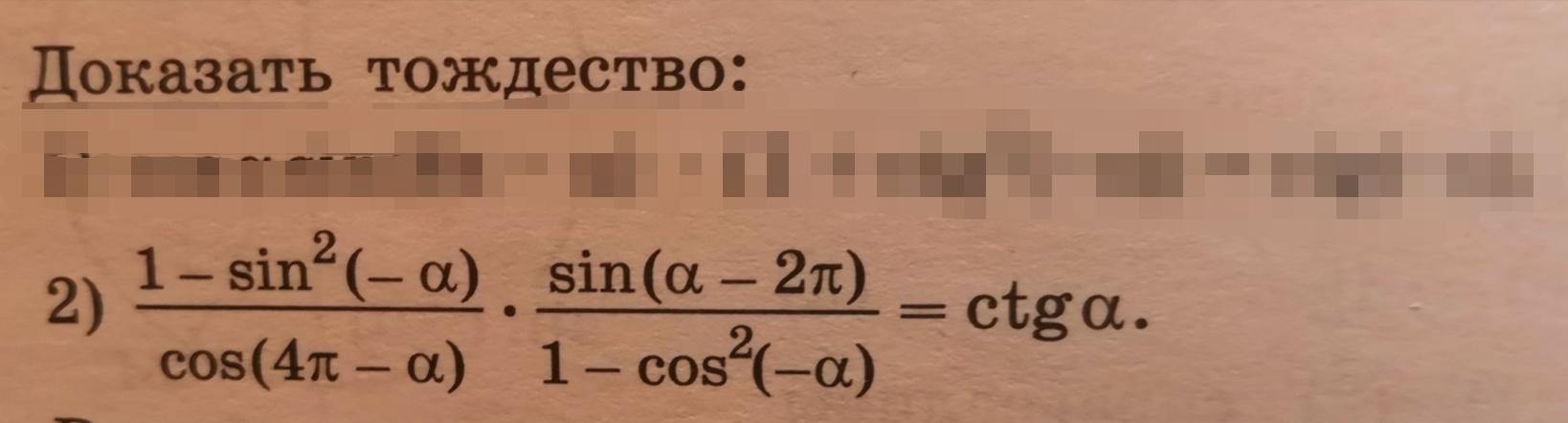
Ответы
Автор ответа:
1
2) α - угол третьей четверти, значит tgα > 0
4) α - угол третьей четверти, значит Cosα < 0
Тождество доказано
Похожие вопросы
Предмет: История,
автор: ramazanmamedemin
Предмет: Алгебра,
автор: sunnysony
Предмет: Математика,
автор: ergesovaaana
Предмет: История,
автор: kamillapantel8
Предмет: Алгебра,
автор: nemtsova82