Предмет: Алгебра,
автор: 111111DA
Не знаю, как решить, весь день решаю....помогите
Приложения:
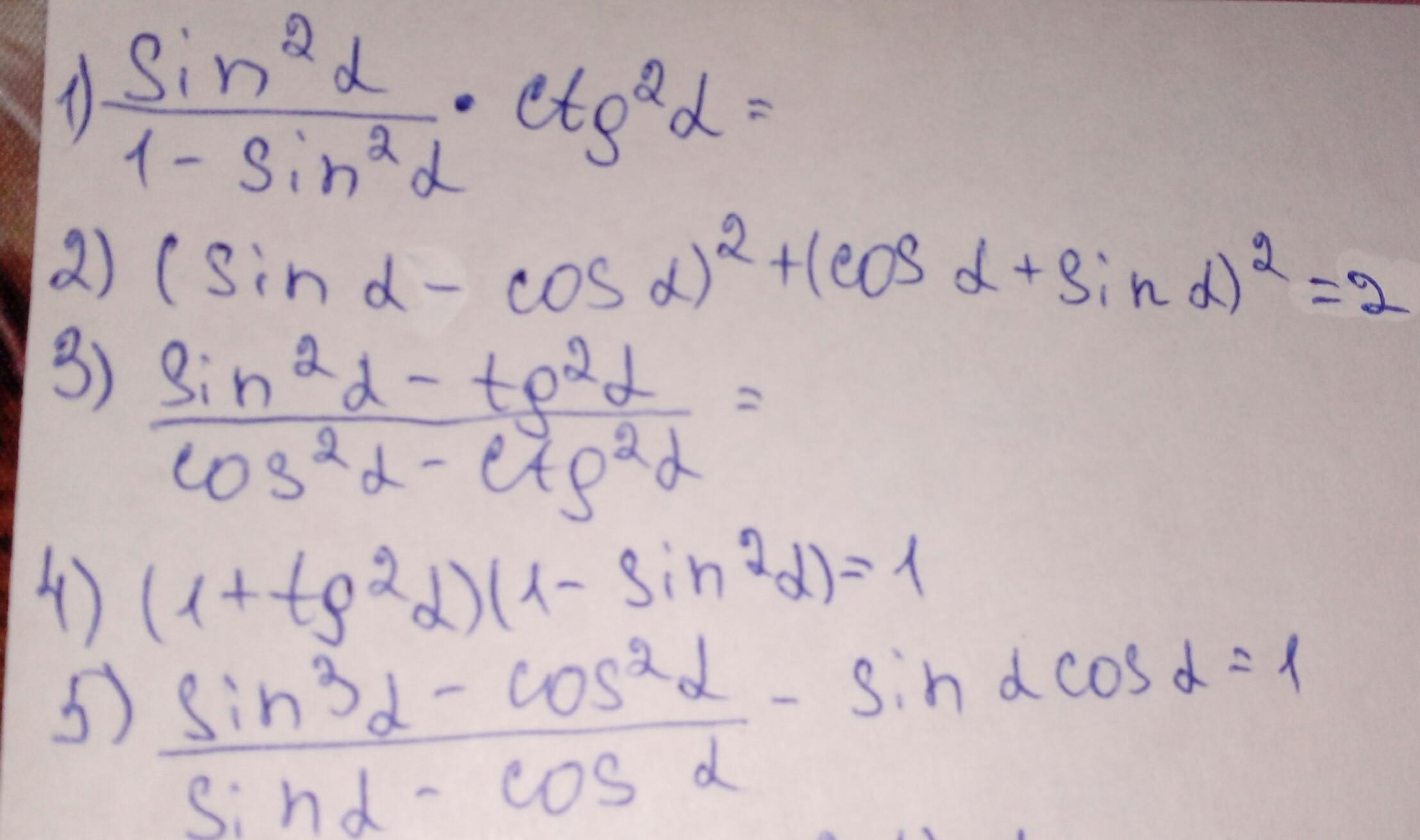
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Информатика,
автор: HuggyWuggy6666
Предмет: Алгебра,
автор: suxotin0743
Предмет: Русский язык,
автор: 6a6akapa
Предмет: Литература,
автор: Аноним