Question

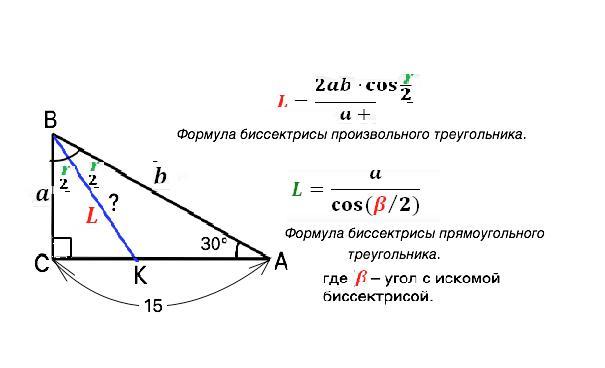
У прямокутному трикутнику катет довжиною 15 см прилягає до кута 30°. Знайдіть більшу бісектрису другого гострого кута трикутника.

Answer 1

 В прямоугольном треугольнике катет длиной 15 см прилегает к углу 30°. Найдите биссектрису большего острого угла треугольника.

——

Ответ: 10 см

Пошаговое объяснение:

Пусть данный треугольник АВС, угол С=90°, ВК - биссектриса, АС=15 см.  угол А=30° .

Сумма острых углов прямоугольного треугольника 90° ⇒

∠В=90-30=60°.

Катет, противолежащий углу 30°, равен половине гипотенузы.

Способ 1)

Примем ВС=х, тогда гипотенуза АВ=2х.

По т.Пифагора АВ²=AC²+BC²⇒

4х²=225+х²

3х²=225 ⇒ х=5√3=ВС;  АВ=2х=10√3

Из ∆ КВС по т.Пифаогора получим ВК=10 см.

——————

Способ 2)

Подставим найденные длины катета и гипотенузы в формулу биссектрисы прямоугольного треугольника

L=a:(cosβ/2)

L=5√3:(√3/2)=10 см.

——————

Способ 3)

В ∆ ВСК сторона ВК - гипотенуза,  угол СВК=30° ( т.к. ВК - биссектриса угла 60°).

Поэтому ВК=ВС:cosCВК=(5√3):√3/2=10 см