Предмет: Алгебра,
автор: gxjdguw
Увага! Завдання на фото.
Приложения:
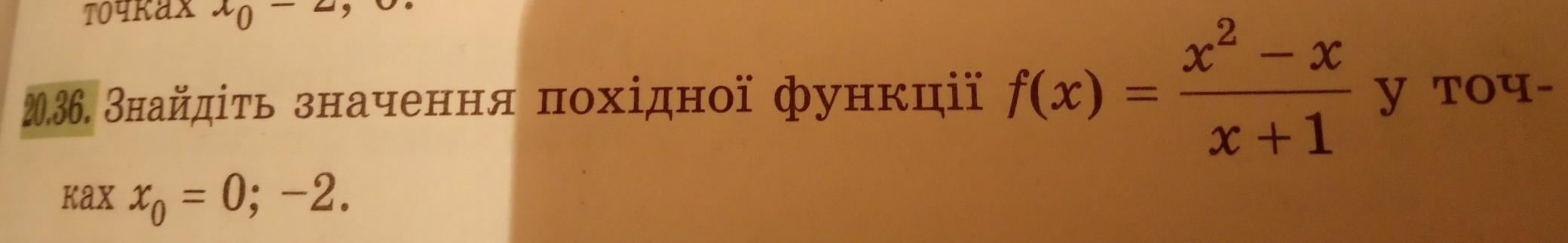
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: Nevoula
Предмет: Английский язык,
автор: Dima15890
Предмет: Математика,
автор: golovinstas63
Предмет: Физика,
автор: Кристина3214
Предмет: Математика,
автор: kimRoma1