Предмет: Алгебра,
автор: TequilaSunrise
помогите, пожалуйста, прошу! желательно через плоскость aox (но можно и любым другим способом)
Приложения:
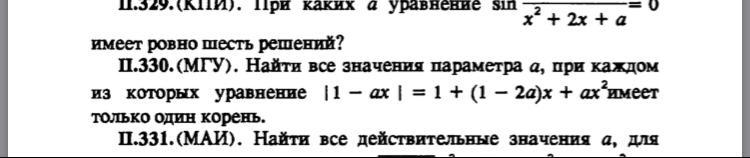
Ответы
Автор ответа:
2
Раскрываем модуль по определению:
1-ax ≥0 ⇒ ax ≤ 1
Уравнение принимает вид:
1-ax=1+(1-2a)x+ax^2
ax^2+(1-a)x=0
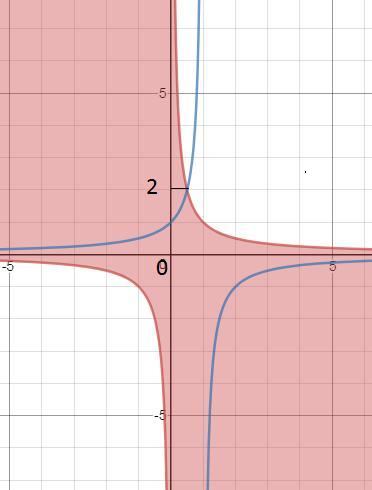
На плоскости хOа
ax ≤ 1 ⇒ a≤1/x- область между двумя ветвями гиперболы a=1/x
ax^2+(1-a)x=0 ⇒ ax^2+x-ax=0 ⇒ a·(x^2-x)=-x ⇒ a=-1/(x-1)
Уравнение имеет решение в области при
a∈(-∞;0)U(0;2]
см. рис.1
1-ax < 0 ⇒ ax > 1
Уравнение принимает вид:
-1+ax=1+(1-2a)x+ax^2
ax^2+(1-3a)x+2=0
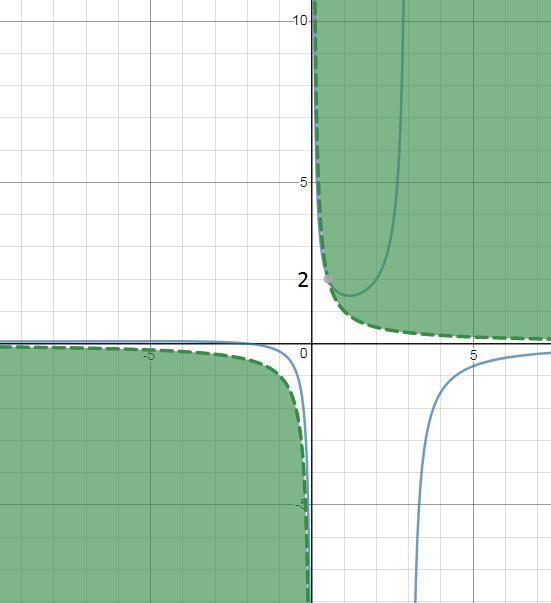
На плоскости хOа
ax > 1 ⇒ a> 1/x- внешняя часть гиперболы a = 1/x
ax^2+(1-3a)x+2=0 ⇒ ax^2+x-3ax+2=0 ⇒ a·(x^2-3x)=-x-2 ⇒ a=-(х+2)/(x^2-3x)
Исследуем функцию с помощью производной и строим график.
Уравнение имеет решение в области при
a∈(-∞;0)U [2;+∞)
см. рис. 2
Ответ. a∈(0;2) U(2;+∞)
Приложения:
Похожие вопросы
Предмет: История,
автор: polinapolina369
Предмет: Английский язык,
автор: zzzzzzzzzzzdas41
Предмет: География,
автор: dccheap91
Предмет: Биология,
автор: romanyuk03