Предмет: Математика,
автор: dmasya
))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
Приложения:
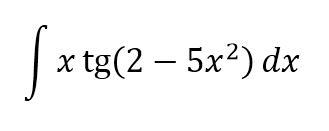
dmasya:
найти интеграл используя интегрирование по частям
интегрируется через замену переменной, интегрирование по частям здесь не пойдет.
у меня в контрольной так написано
и ничего не получается
в итоге 0 выходит
Ответы
Автор ответа:
2
Ответ:
(1/10)ln|cos(2-5x^2)|+C
x^2=t 2xdx=dt
тогда интеграл примет вид 1/2Int(tg(2-5t)dt=1/2Int(sin(2-5t)/cos(2-5t))dt
вспомним, что (cost)'=-sin(t)
=1/2ln|cos(2-5t)|*1/5=(1/10)ln|cos(2-5t)|+C
возвращаемся к старой переменной
=
Пошаговое объяснение:
x^2=t 2xdx=dt
тогда интеграл примет вид 1/2Int(tg(2-5t)dt=1/2Int(sin(2-5t)/cos(2-5t))dt
вспомним, что (cost)'=-sin(t)
=1/2ln|cos(2-5t)|*1/5=(1/10)ln|cos(2-5t)|+C
возвращаемся к старой переменной
=(1/10)ln|cos(2-5x^2)|+C
Похожие вопросы
Предмет: Математика,
автор: reie304
Предмет: Биология,
автор: diana1557poop
Предмет: Физика,
автор: alionavas2007
Предмет: Физика,
автор: ГрустныйПирожок
Предмет: Математика,
автор: имани8