Question

3.
Вариант 4
Из точки M, которая лежит вне плоскости а, проведены к этой пло-
скости наклонные MN и МК, образующие с ней углы 30° и 45° соот-
ветственно. Найдите длину наклонной MK, если длина проекции на-
клонной MN на плоскость а равна 4корней из 3 см.
2.Точка М принадлежит одной из граней двугранного угла и удалена от
его ребра на 4 см. Найдите расстояние от точки M до другой грани уг-
ла, если величина этого угла равна 45°.
Угол между плоскостями ABC и ADC равен 60°, AB = BC = AC = 12 см,
AD= CD, ZADC = 120°. Найдите отрезок BD.
3.Концы отрезка, длина которого равна 14 см, принадлежат двум пер-
пендикулярным плоскостям, а расстояния от его концов до линии пе-
ресечения плоскостей равны 8 см и 5 см. Найдите расстояние между
основаниями перпендикуляров, опущенных из концов отрезка на ли-
нию пересечения плюскостей.
5.Через сторону правильного треугольника проведена плоскость, кото-
рая образует с двумя остальными сторонами треугольника углы по
30°. Найдите синус угла между плоскостью данного треугольника и
проведённой плоскостью.
Решите пожалуйста, что можете.... ​

Answer 1

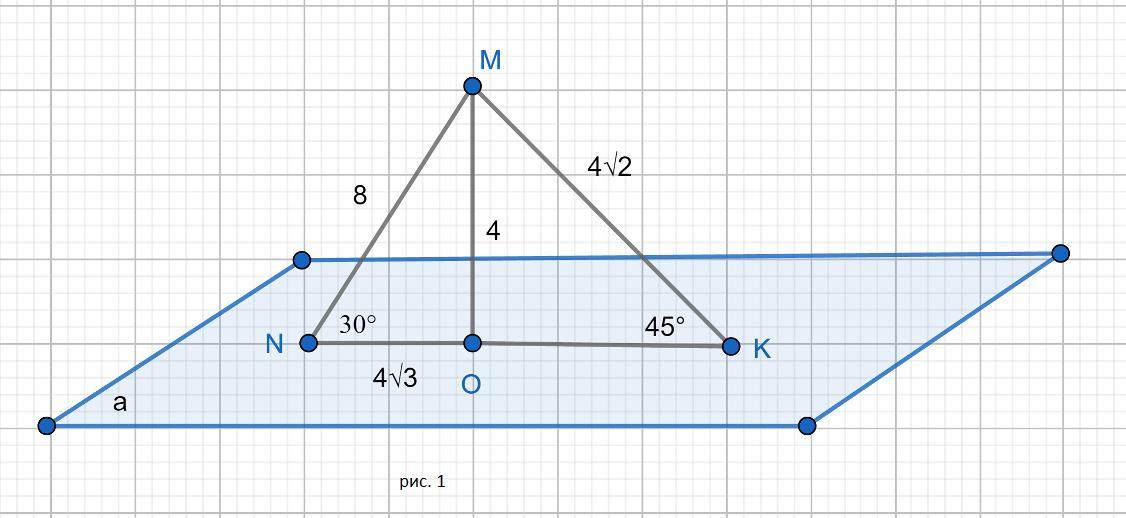
1. В треугольнике MNO ∠N = 30°, ∠O = 90°, сторона NO = 4√3 по условию/ Найдем сторону MN:

Cos 30° = NO/MN = √3/2;   ⇒   4√3/MN = √3/2;    ⇒   MN  = 4√3 * 2 / √3 ;

MN = 8 см.  Тогда MO = 4 см. (катет, лежащий против угла 30° = половине гипотенузы).

В треугольнике MOK ∠O = 90° ; ∠K = 45°,  тогда ∠M = 45°.  ⇒ Треугольник MOK равнобедренный и OK = 4 см.

По т.Пифагора МК = √(16+16) = 4√2 см.

Ответ: MK = 4√2 см.