Предмет: Алгебра,
автор: ALDR5
Решить интеграл методом универсальной тригонометрической подстановки ( Номер 9 )
Приложения:
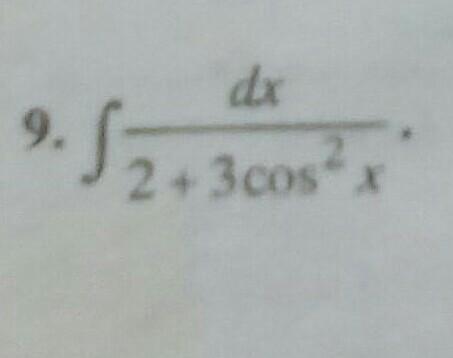
Ответы
Автор ответа:
0
2+3cos^2x=2+3/2(1+cos2x)
dx/(2+3cos^2x)=2dx/(7+3cos2x)
tgx=t cos2x=(1-t^2)/(1+t^2)
dx=2/(1+t^2)
(4/(1+t^2))/(7+3(1-t^2)/(1+t^2))=2/(5+2t^2)
2/5(1+((√2/5)t)^2
интеграл = 2/5*arctg(sqrt(0,4)t)*sqrt(5/2)=sqrt(0.4)arctg(sqrt(0.4)t)
обратная замена
ответ sqrt(2/5)*arctg(sqrt(2/5)tgx)+C
Похожие вопросы
Предмет: Биология,
автор: maruseka8283
Предмет: ОБЖ,
автор: bamary
Предмет: Химия,
автор: linda3avr
Предмет: Геометрия,
автор: mishajust
Предмет: Математика,
автор: даня5553