Question

Срочно!
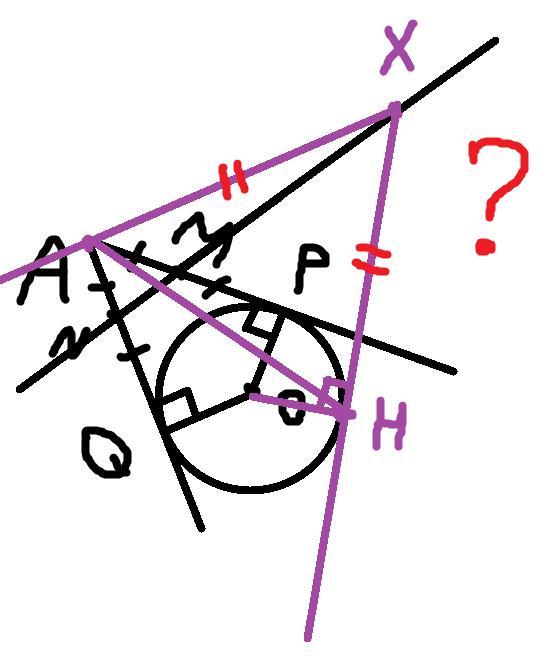
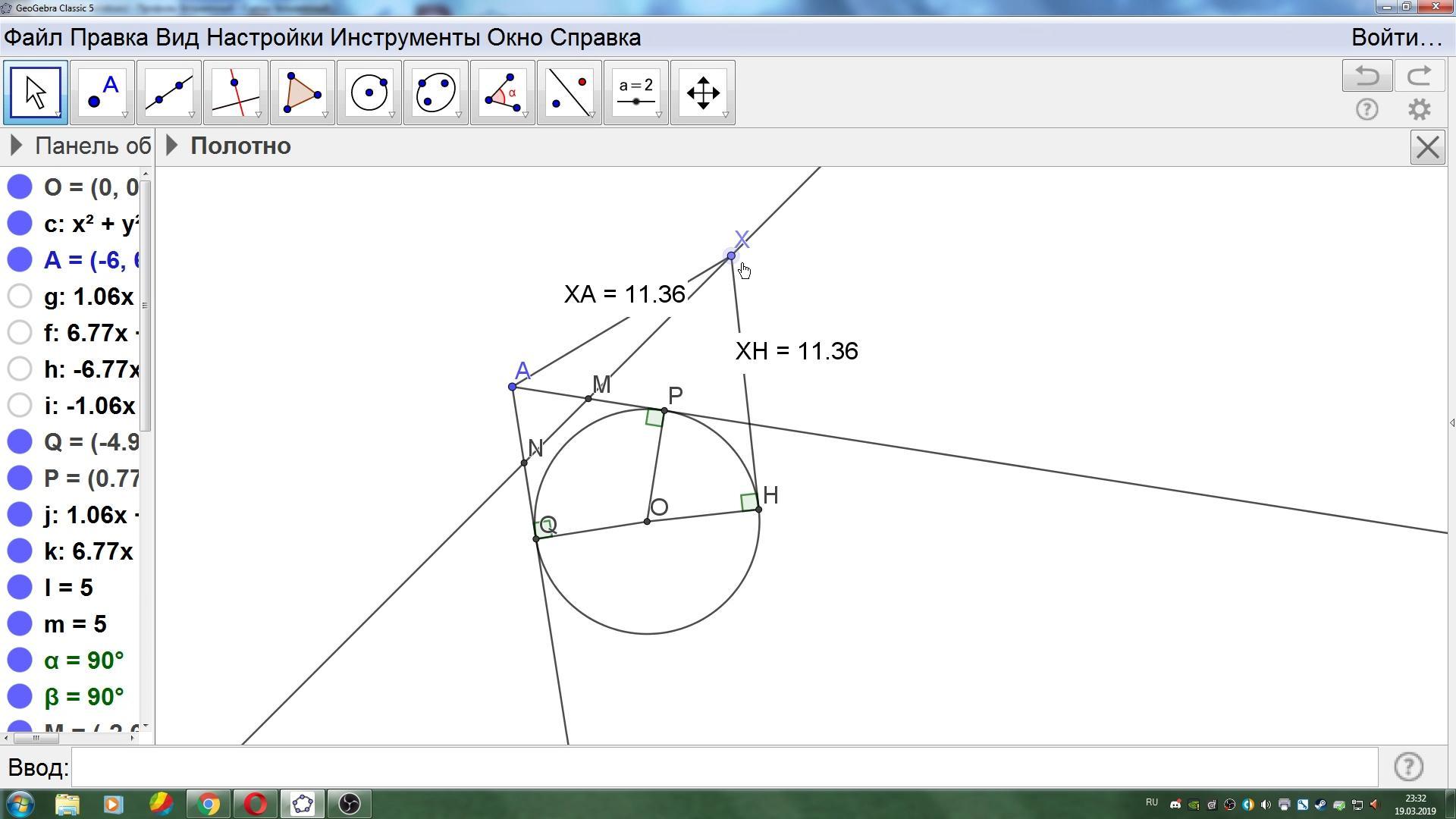
Из точки A проведены касательные AP и AQ к окружности. Точки M и N - середины отрезков соответственно. На прямой MN взяли произвольную точку X. Докажите, что длина отрезка касательной, проведенной из X к окружности, равна длине отрезка AX.

Answer 1

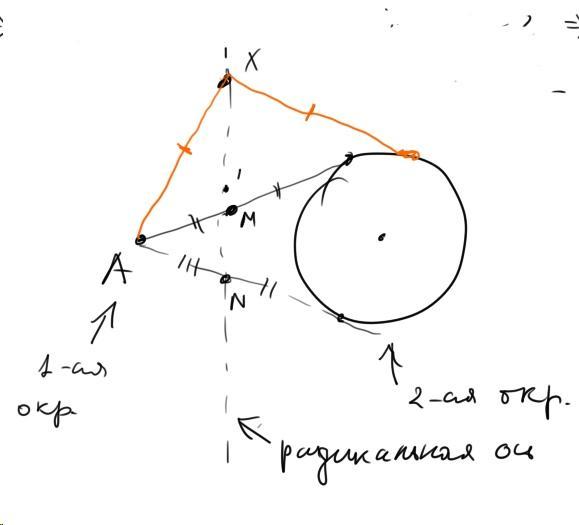
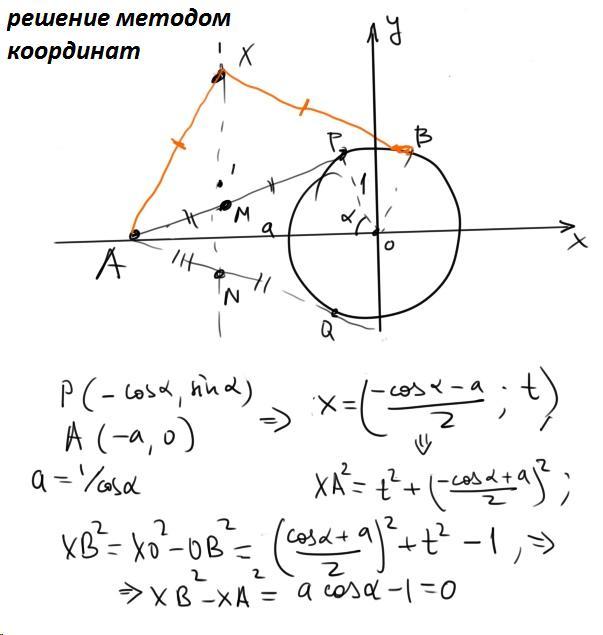
Если у вас есть две окружности, и вы возьмете все точки, такие, что куски касательных из них к этим окружностям равны, то эти точки будут образовывать прямую, которая называется радикальной осью двух окружностей. Поэтому в вашей задаче у вас тоже две окружности, только вторая окружность имеет радиус 0 и выродилась в точку А. Точки N и M - это две точки, куски касательных от которых к этим окружностям равны. Значит, они лежат на радикальной оси. Значит, прямая MN и есть радикальная ось. А значит куски касательных от любой точки на ней до окружностей равны.