Question

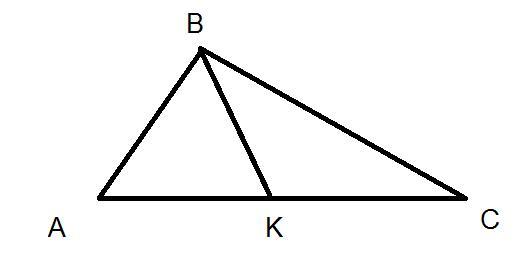
В ΔABC (рисунок) на стороне AC взята точка K, AK=BK=KC, ∠ABK=58°. Найдите ∠CBK (Просьба сделать всё с решением).

Answer 1

Вершины △ABC равноудалены от точки K т.к. AK=BK=KC ⇒ K - центр описанной окружности;

• Вписанный угол, опирающийся на диаметр окружности, равен 90°.

AC - диаметр т.к. содержит центр окружности - точку K.

∠ABC = 90° т.к. опирается на диаметр AC и является вписанным;

∠CBK+∠ABK = ∠ABC т.к. они составляют этот угол;

∠CBK = ABC-∠ABK;

∠CBK = 90°-58° = 32°.

Ответ: 32°.