Предмет: Алгебра,
автор: sergeevajw
Найти наибольшее и наименьшее значение функции на отрезке [а, b]
Приложения:
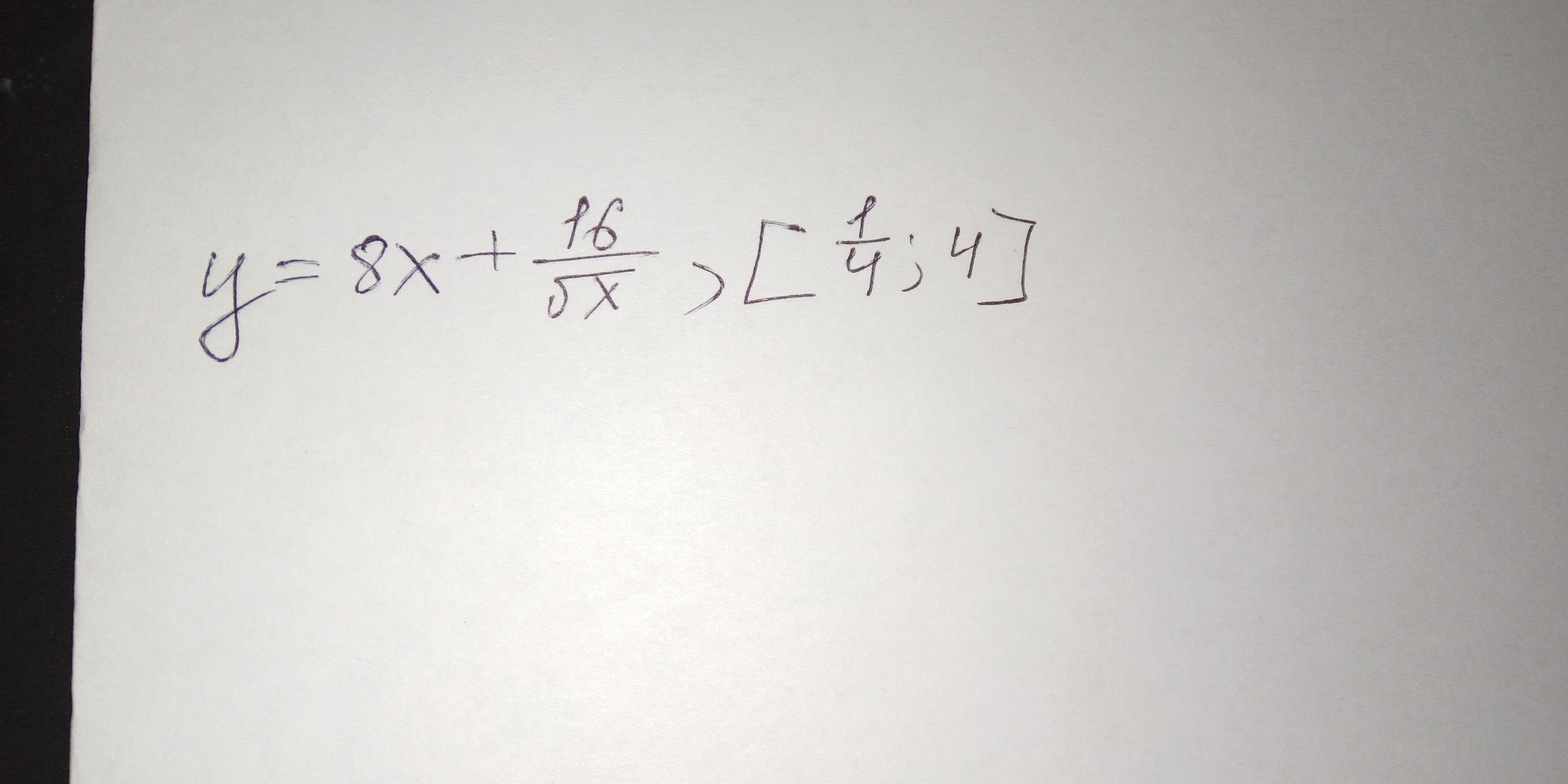
Ответы
Автор ответа:
0
Переменная х не принимает отрицательных значений.
Производная равна y' = 8 - (8/x^(3/2)) = (8*x^(3/2) - 8)//x^(3/2)).
Приравняем её нулю (достаточно числитель, х не равен 0):
8*x^(3/2) - 8 = 0, или, сократив на 8: x^(3/2) - 1 = 0.
Отсюда получили одно значение критической точки: х = 1.
Определим её характер по перемене знака:
х = 0,25 1 2
y' = -56 0 5,17157.
Как видим, в точке х = 1 минимум функции (переход с - на +), у = 24.
Теперь находим значения функции на границах заданного промежутка.
x = 0,25 4
y = 34 40.
Максимум на заданном промежутке в точке х = 4, у = 40.
Похожие вопросы
Предмет: Геометрия,
автор: natan2022
Предмет: Математика,
автор: tarasuksasa621
Предмет: Математика,
автор: Jhvvvvv
Предмет: Физика,
автор: algebra26
Предмет: Математика,
автор: Аноним