помогите решить, пожалуйста
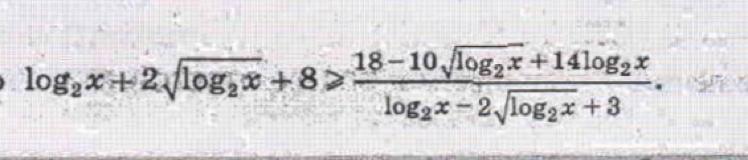
Ответы
Введём новую переменную √log₂x = t, тогда log₂x = t².
теперь наше неравенство:
t² +3t+8 ≥ (18 -10t +14t²)/(t² -2t +3)
t² +3t+8 - (18 -10t +14t²)/(t² -2t +3) ≥ 0
((t² +3t+8 )(t² -2t +3) - (18 -10t +14t²) )/ (t² -2t +3) ≥ 0
(t⁴ +2t³ +8t² -2t³ -4t² -16t +3t² +6t +24 -18 +10t -14t²)/(t² -2t +3) ≥ 0
(t⁴ -7t² +6t)/(t² -2t +3) ≥ 0
метод интервалов.
t⁴ -7t² +6t = 0 t² -2t +3 = 0
t² = z ∅
z² -7z +6 = 0
корни 1 и 6
t² = 1 t² = 6
t = +-1 t = +-√6
Имеем 4 корня "t"
t⁴ -7t +6 = (t-1)(t+1)(t-√6)(t+√6)
Учтём что t²-2t +3 > 0, значит, (t-1)(t+1)(t-√6)(t+√6) ≥ 0
-∞ -√6 -1 1 √6 +∞
+ - - - + это знаки (t-√6)(t+√6)
+ + - + + это знаки (t-1)(t+1)
IIIIIIIIIIIIIII IIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIII это решение
1) t ≤ -√6 2) -1 ≤ t ≤ 1 3) t ≥√6
log₂x ≤ -√6 -1 ≤ log₂x ≤ 1 log₂x ≥√6
x ≤ 2^-√6 1/2 ≤ x ≤ 2 x ≥ 2^√6
ОДЗ: х > 0
Ответ: x ≤ 2^-√6 ; 1/2 ≤ x ≤ 2 ; x ≥ 2^√6 .