Question

В равнобедренном треугольнике основание и проведенная к ней высота равны 48см и 32см.Точка лежит на расстоянии 60см от плоскости треугольника и на одинаковом расстоянии от его вершин.Обчислиты расстояние от этой точки до вершин треугольника.

Answer 1

NO=60, AH=32,  BC=48, AN=BN=CN, Найти AN
АО=ОВ=ОС. Пусть АО=ОВ=х, ОН=32-х, Из треугольника ОВН имеем
$24^{2}+(32-x)^{2} = x^{2};64x=1600;x=25$
Из треугольника AON получаем $AN= sqrt{625+3600}= sqrt{4225}=65$.

82ec0e0e25279c198ec81e91c66977b1.docx

Answer 2

В равнобедренном треугольнике основание и проведенная к нему высота равны 48 см и 32см соответственно. Точка лежит на расстоянии 60 см от плоскости треугольника и на однаковом расстоянии от его вершин. Вычислите расстояние от этой точки до вершин  треугольника .
 ===================
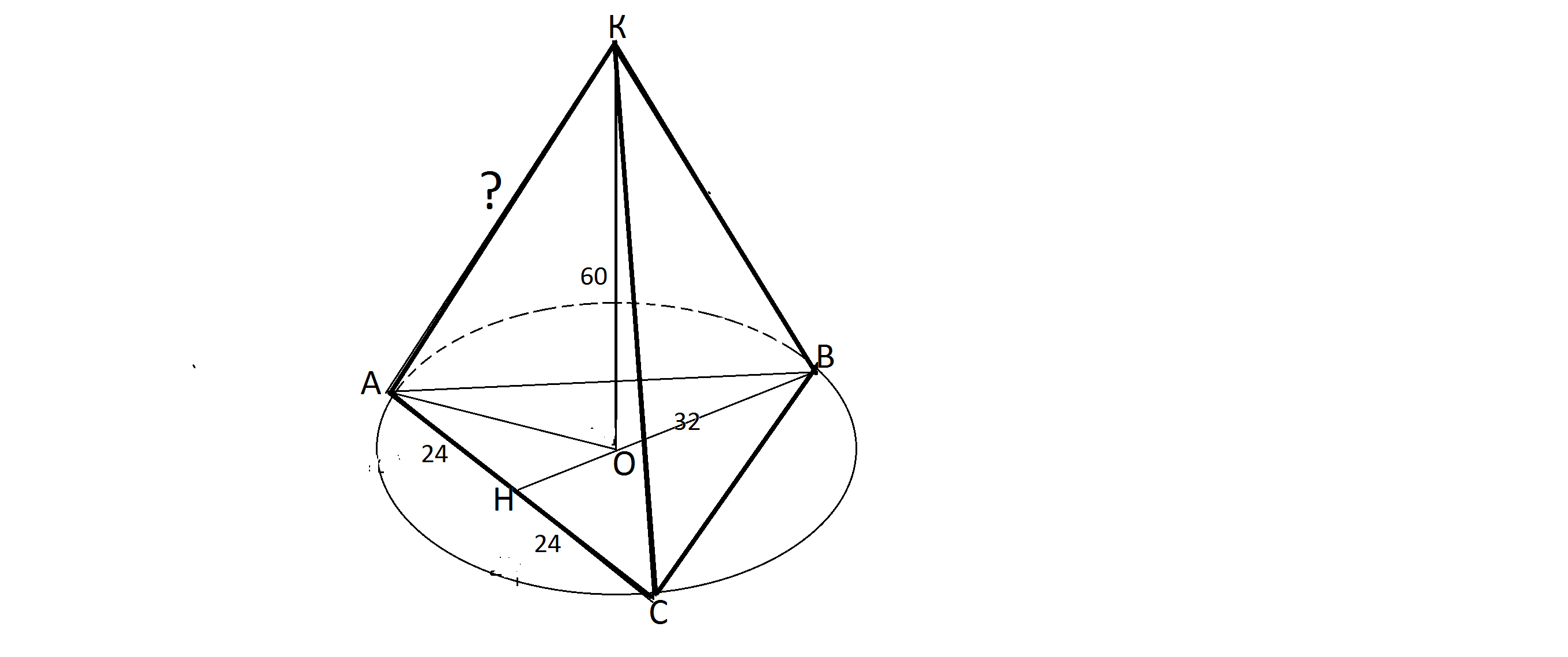
Сделаем рисунок и обнаружим, что у нас получилась треугольная пирамида,
 в основании которой лежит равнобедренный треугольник. 
КО- высота этой пирамиды, т.к является расстоянием от точки К до плоскости треугольника ( расстояние измеряется перпендикуляром). 
Так как вершина пирамиды лежит на одинаковом расстоянии от вершин треугольника АВС, все ее ребра равны и проекции этих ребер тоже равны.
 КА=КВ=КС 
ОА=ОВ=ОС Эти проекции равны радиусу описанной вокруг треугольника АВС окружности. 
Нужное расстояние можно найти из прямоугольного треугольника АОК. 
Для того, чтобы найти радиус описанной окружности, нужно найти стороны АВ и ВС треугольника АВС. 
ВН - высота АВС
Треугольник АВН прямоугольный. 
По т. Пифагора найдем АВ. 
АВ=√(ВН²+АН²)=√(24²+32²)=20 см
По формуле радиуса описанной окружности вокруг равнобедренного треугольника найдем длины проекций ребер пирамиды. 
R=а²:√(4а²-b²)=40²:√( 6400-2304)=25 см 
АК=√(25²+60²)=65 см
Ответ - точка удалена от вершин треугольника на 65 см