Предмет: Геометрия,
автор: banachi89
В треугольнике ABC угол C=90, AC=5 , высота CH равна 3 . Найдите cosb
Ответы
Автор ответа:
3
Пусть сторона СВ = у, а сторона НВ = х. Из треугольника АВС получаем по теореме Пифагора:
х²+9=у²;
Из треугольника НВС по теореме Пифагора:
25+у²=(4+х)²;
Решаем эту систему. Прибавляем к первому уравнению второе и получаем:
х²+9+25=16+2х+х²;
2х=18;
х = 9.
у²=90 ⇒ у = 3√10.
cosB=х/у = 9/3√10 = 3/√10
Автор ответа:
2
cosB=sinA
∠CHA=90° ⇒ ΔCHA - прямоугольный, т.к. СН - высота.
АН² = АС² - СН²
АН = √(25-9)= √16 = 4
⇒ sinА = cosB = СН / АС = 3 / 5 = 0,6
Ответ: 0,6
Приложения:
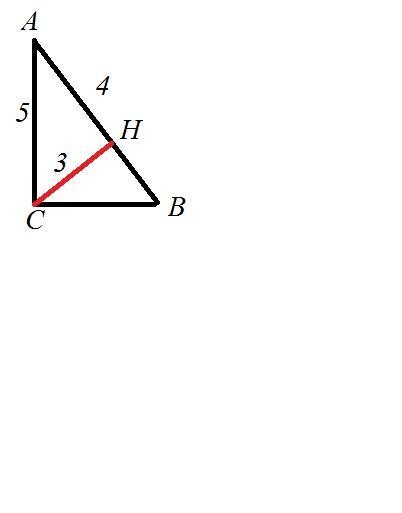
Похожие вопросы
Предмет: Алгебра,
автор: garipovaliusha
Предмет: Алгебра,
автор: nikolay4016
Предмет: Русский язык,
автор: azizazumakiseva2
Предмет: Физика,
автор: Luki0
Предмет: Литература,
автор: fari010