Предмет: Геометрия,
автор: ssahasgsh
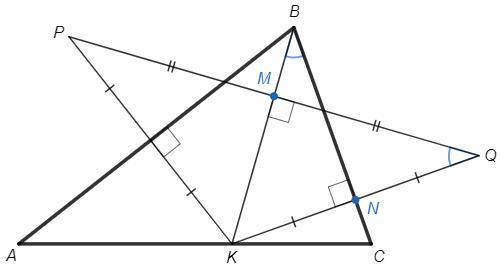
В треугольнике ABC на стороне AC выбрали точку K. Точки P и Q симметричны точке K относительно сторон AB и BC. Оказалось, что прямая BK делит отрезок PQ пополам. Докажите, что угол KBC равен одному из углов треугольника KPQ
Ответы
Автор ответа:
0
Симметрия точек относительно прямой - это симметрия концов отрезка относительно серединного перпендикуляра. AB и BC - серединные перпендикуляры в треугольнике PKQ. Серединные перпендикуляры треугольника пересекаются в одной точке. Следовательно, прямая, проходящая через точку пересечения серединных перпендикуляров (B) и середину отрезка PQ, является перпендикуляром к PQ.
Пусть M - середина PQ, N - середина KQ. Треугольники KBN и KQM подобны (прямоугольные с общим углом), ∠KBC=∠KQP.
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: nikonovaviktoria081
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: sashashtukun805
Предмет: Информатика,
автор: velbok
Предмет: Алгебра,
автор: Nastradamsik