Предмет: Алгебра,
автор: DearStefani
СРОЧНО ПОМОГИТЕ!!! Найти производную
Приложения:
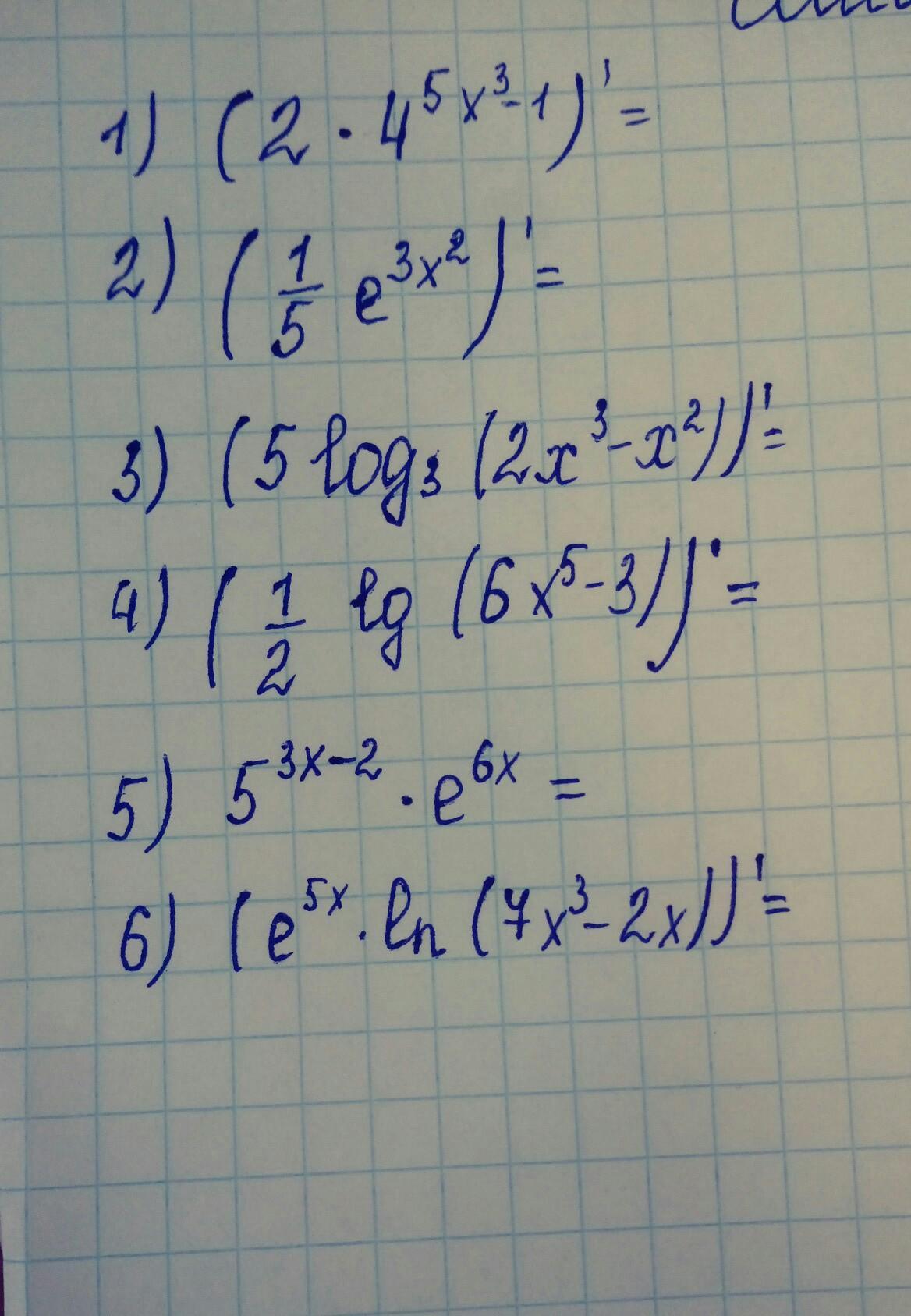
Ответы
Автор ответа:
1
Решение во вложении.
Приложения:

Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: garipovaliusha
Предмет: Английский язык,
автор: wergnazarov
Предмет: Физика,
автор: hotel18897
Предмет: Информатика,
автор: заялупси
Предмет: Математика,
автор: кнег755568