Question

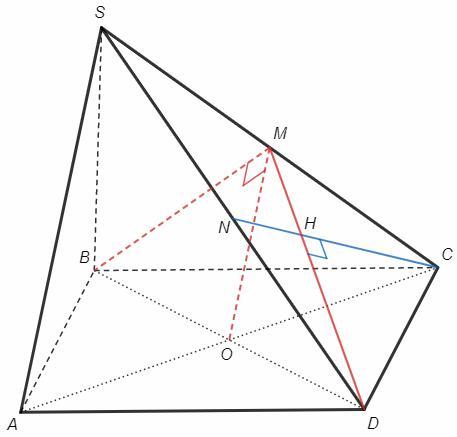
Основание пирамиды SABCD – параллелограмм ABCD , точки M и N – середины рёбер SC и SD соответственно. Прямые SA , BM и CN попарно перпендикулярны. Найдите объём пирамиды, если SA=a , BM=b , CN=c .

Answer 1

O - точка пересечения диагоналей параллелограмма ABCD.

MO - средняя линия в SCA, MO=SA/2 =a/2

MO||SA => MO⊥BM, S(BMO)=BM*MO/2 =ab/4

MO - медиана, S(BMD)=2S(BMO) =ab/2

H - точка пересечения медиан в DSC, CH=2/3 CN =2/3 c

CN⊥SA => CN⊥MO, CN⊥BM => CN⊥(BMD)

CH - высота в пирамиде CBMD, V(CBMD)=S(BMD)*CH/3 =abc/9

Перпендикуляр из S к плоскости (ABC) вдовое больше перпендикуляра из M, площадь ABCD вдвое больше площади BCD, следовательно S(SABCD)=4S(CBMD) =4/9 abc