Предмет: Алгебра,
автор: BJIADA
Помогите найти производную функции
Приложения:
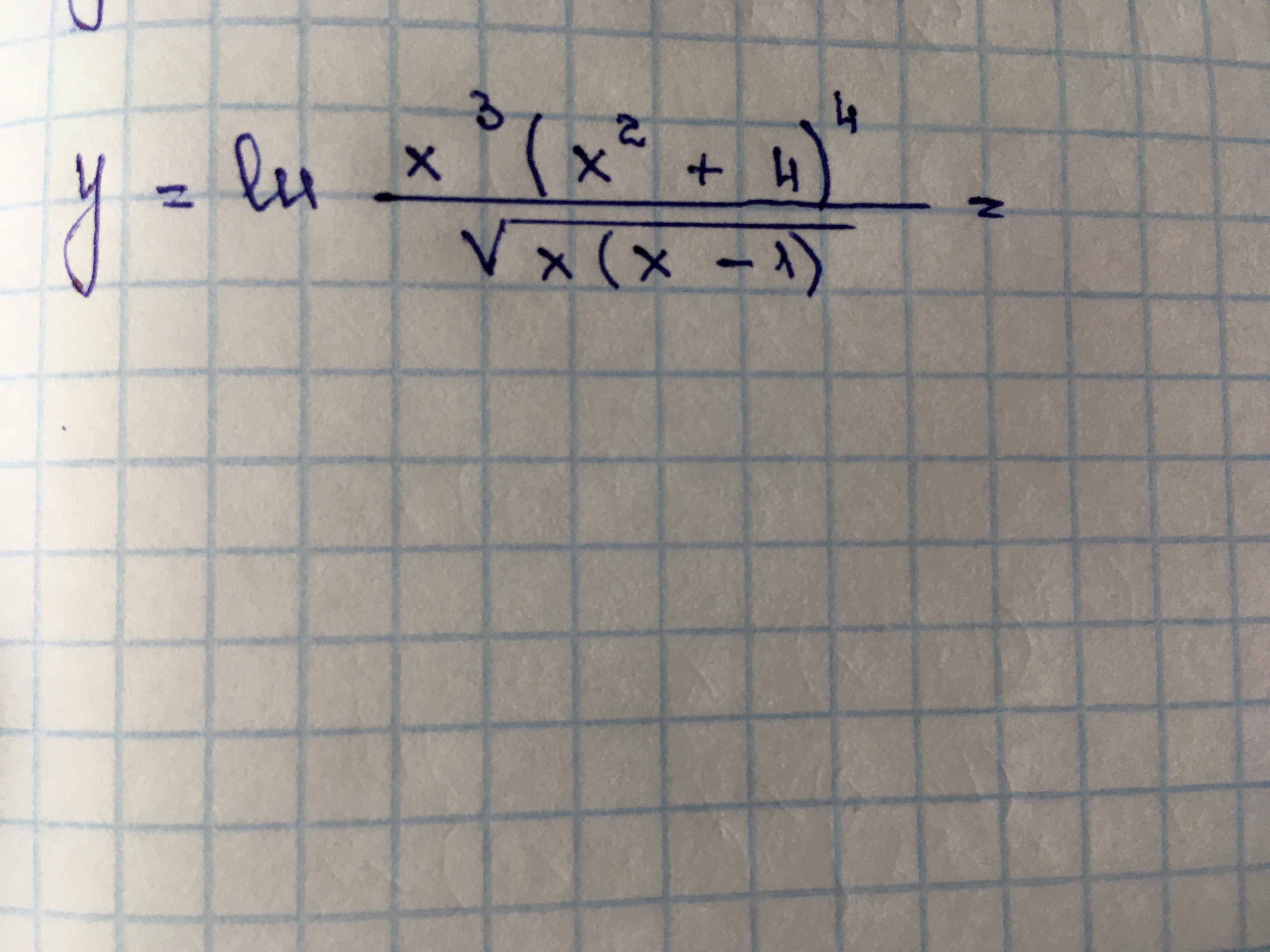
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Музыка,
автор: laktionovaalena291
Предмет: Биология,
автор: figgikfss
Предмет: Математика,
автор: burdjui39
Предмет: Математика,
автор: Котинкина