Предмет: Геометрия,
автор: 1528белка
Дано: треуг ACB-прямоуг.
AD-биссектриса
угол D в треуг ADB=110°
Найти: внешний угол В
Рассмотрим треуг DCA и треуг ACD
угол CAD = угол DAB (т.к. AD - биссектриса)
угол D в треуг ADB=110°
угол D в треуг ACD = 180-110=70° (как смежные)
угол А в треуг CAD=180-(90+70) = 20° ⇒
рассмотрим треуг ADB
угол D=110°
угол А=20° (биссектриса делит угол А пополам)
угол B=180-(110+20) = 50° ⇒
внешний угол B= 180-50 = 130°
Приложения:
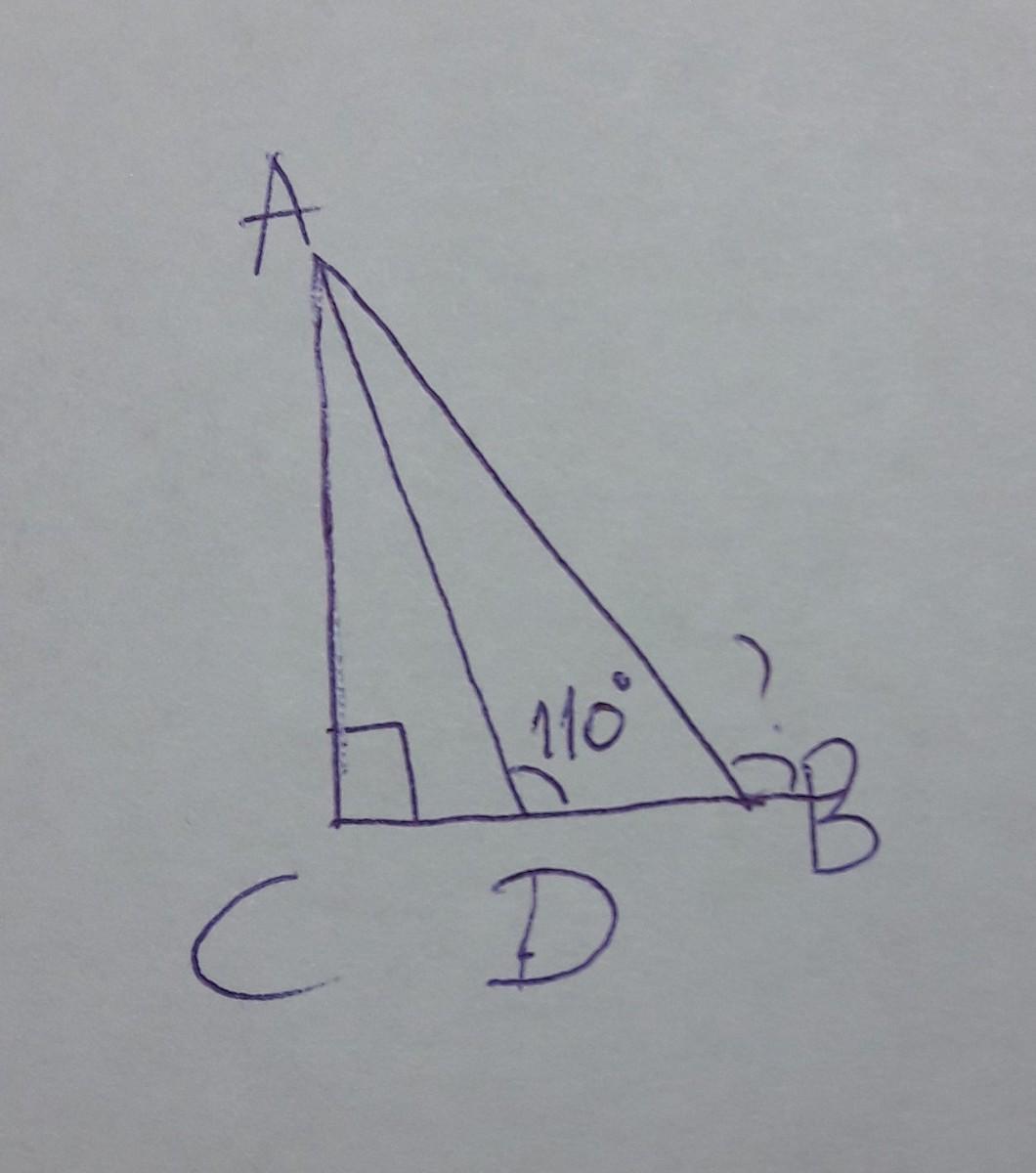
Ответы
Автор ответа:
0
Не 130 градусов , а 150 , так как биссектриса делит угол пополам , получаем А=20*2=40 , а внешний угол равен сумме двух углов треугольника не смежных с ним , отсюда следует , что В=40+110=150 градусов . Ответ:внешний угол В равен 150 градусам
Похожие вопросы
Предмет: Физика,
автор: anzelikabazenova85
Предмет: Математика,
автор: 89097506029rai
Предмет: Українська література,
автор: artem534604
Предмет: Литература,
автор: юлия1387