Предмет: Алгебра,
автор: Galinka23
Помогите пожалуйста решить
Приложения:
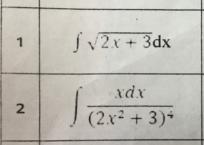
HSS9860:
Оба интеграла можно взять путём подведения под знак дифференциала; в первом получиться должно "1/3 *sqrt((2x+3)^3)+C"; во втором '-1/(12 * (2x^2+3)^{-3}) +C'.
спасибо я уже решила только в первом ответ другой
Ответы
Автор ответа:
4
1.
замена переменной:
2x+3=u
x=(u-3)/2
dx=(1/2)du
∫√(2x+3)dx=∫√u·(1/2)du=(1/2)∫√u du=
2.
замена переменной:
2x²+3=u
(2x²+3)`dx=du
4xdx=du
xdx=(1/4)du
∫xdx/(2x²+3)⁴=∫u⁻⁴·(1/4)du=(1/4)·(u⁻³/(-3))+C = (-1/12)· (1/u³)+C=-1/(12·(2x²+3)³) + C
В ответе для №1 опечатка: вместо u^3 должно было быть u^2 (и далее до конца).
Просьба проигнорировать комментарий "В ответе для...". Или стереть. Спасибо.
Похожие вопросы
Предмет: Биология,
автор: dvxk6gcqmq
Предмет: Українська література,
автор: makarenkosvetlana201
Предмет: Физика,
автор: Аноним
Предмет: Обществознание,
автор: KwonJiyong
Предмет: История,
автор: zOnG337