Предмет: Алгебра,
автор: Аноним
Напишите подробное решениею
Приложения:
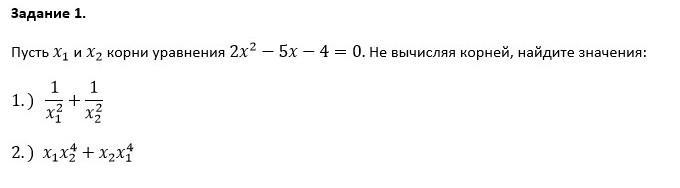
Ответы
Автор ответа:
1
Воспользуемся теоремой Виета.
Похожие вопросы
Предмет: Математика,
автор: amik7672
Предмет: Қазақ тiлi,
автор: dzorikaru
Предмет: Физика,
автор: romanofkozelin
Предмет: Литература,
автор: dimaandreevich
Предмет: Литература,
автор: Annareks