Предмет: Алгебра,
автор: ttmsee
помогите,пожалуйста, с подробным решением
Приложения:
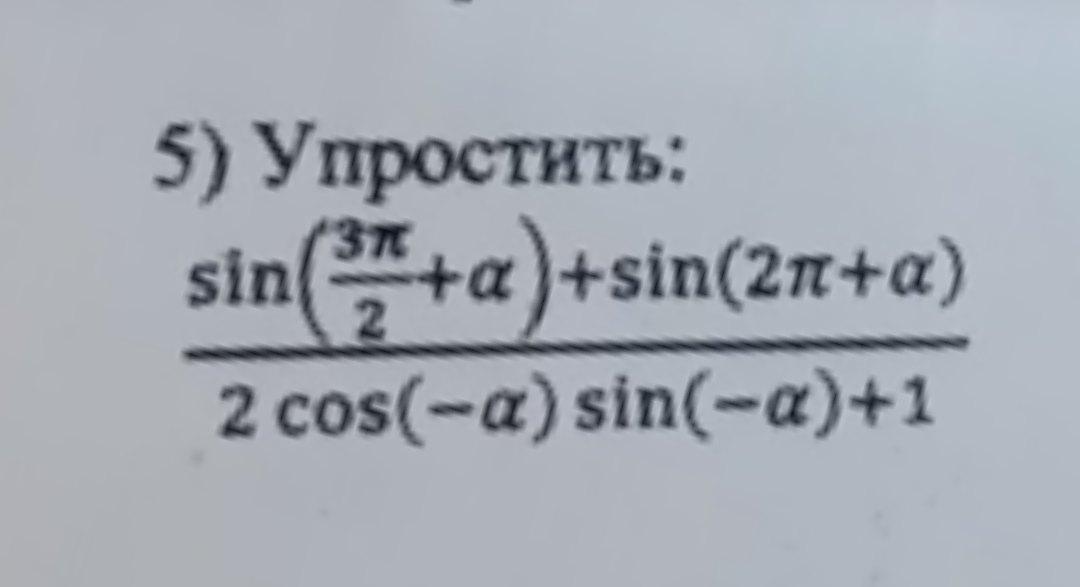
Ответы
Автор ответа:
0
P.S.
Похожие вопросы
Предмет: Биология,
автор: mirphone1710
Предмет: Литература,
автор: maksimtars
Предмет: Геометрия,
автор: dropblyd
Предмет: Математика,
автор: Yevaa
Предмет: Литература,
автор: NastyaOLO