Question

50 БАЛЛОВ
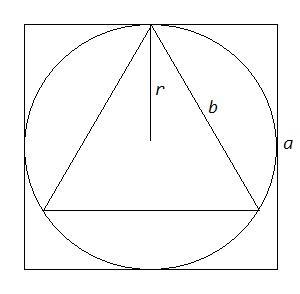
Найти площадь квадрата, описанного вокруг окружности, если площадь правильного треугольника, вписанного в этот круг, равна 9√3 см²

Answer 1

Радиус описанной окружности правильного треугольника

r= b √3/3

Площадь правильного треугольника

Sт= b^2 √3/4

Радиус вписанной окружности квадрата

r= a/2

Площадь квадрата

Sк= a^2 =4r^2 =4 *b^2/3 = 4/3 *4/√3 *Sт =4/3 *4/√3 *9√3 =48 (см^2)