Предмет: Математика,
автор: krop40
допожіть розв'язати нерівність
Приложения:
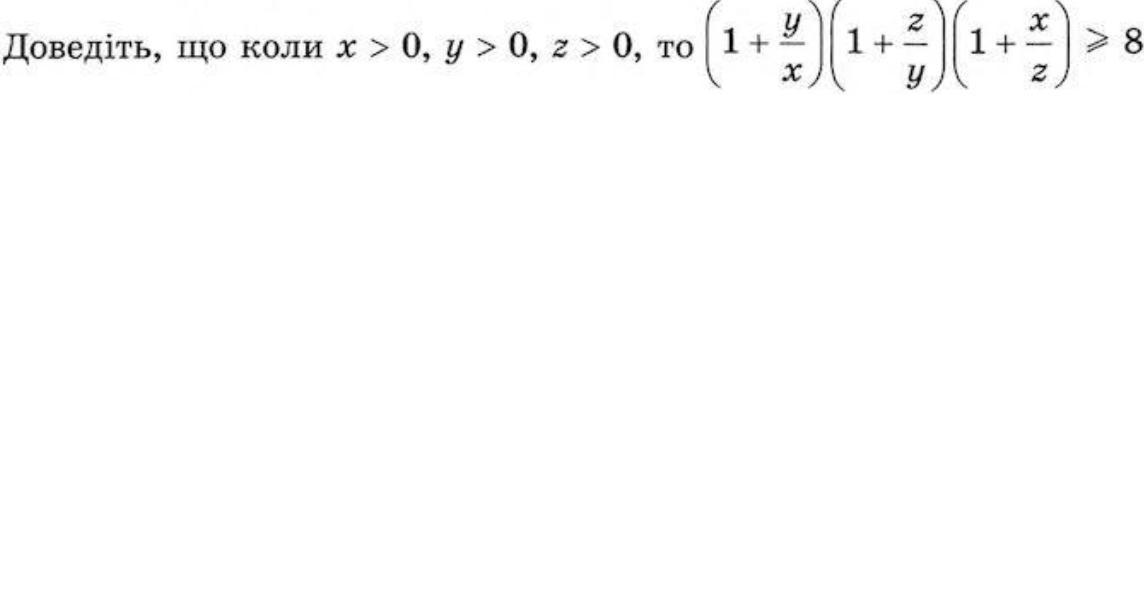
Ответы
Автор ответа:
1
Применяем неравенство Коши-Буняковского
(√a-√b)²≥0
a - 2√(ab) + b ≥0
Перемножаем:
Похожие вопросы
Предмет: Алгебра,
автор: ttana6297
Предмет: Литература,
автор: 09krasotulka
Предмет: Математика,
автор: Diana37011
Предмет: Физика,
автор: Артем2016111
Предмет: Математика,
автор: buumbuck