Предмет: Алгебра,
автор: ramazan0124
найдите значение выраженияпомогите пожалуйста
Приложения:
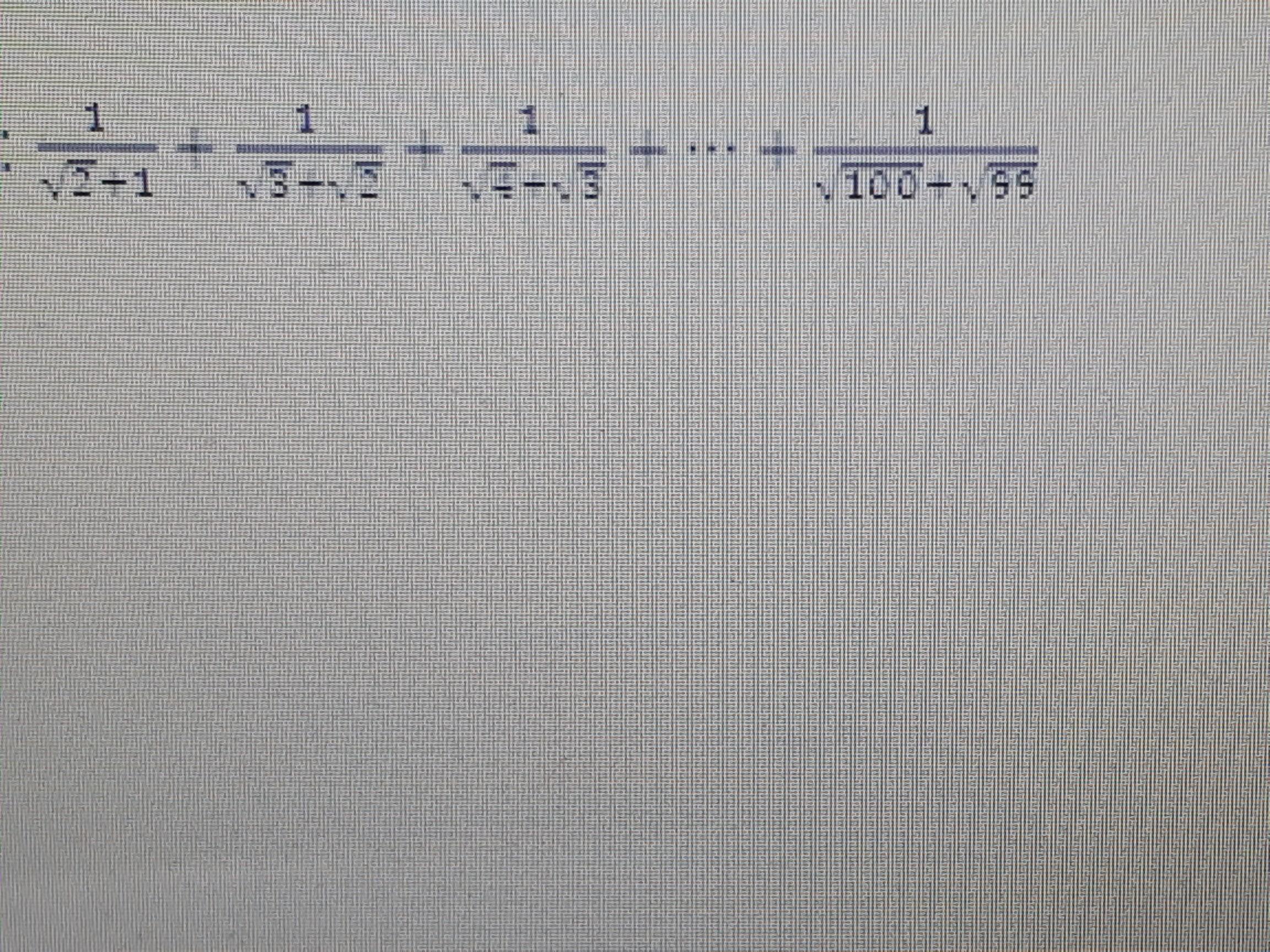
Ответы
Автор ответа:
0
Все корни, начиная с √2 и заканчивая √99 присутствуют в последнем выражение как со знаком плюс, так и со знаком минус, а значит в сумме будут давать ноль.
Таким образом, получим, что значение выражения равно
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: fpxuyiduyduyfih
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: Аноним
Предмет: Алгебра,
автор: maksvashlaev
Предмет: Математика,
автор: григори3