Предмет: Математика,
автор: dasha29293
Срочно!!!!! Дам 50 баллов.
Только с нормальным решением
Приложения:
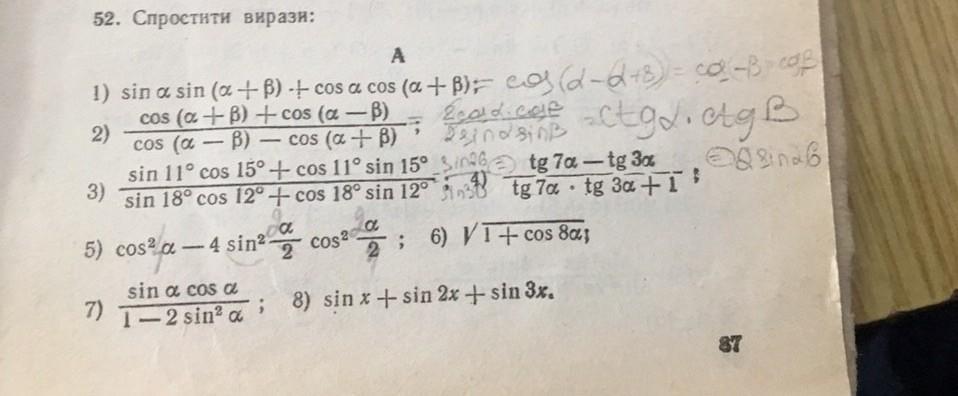
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: vasilisarozova
Предмет: Русский язык,
автор: arturnagaev1234
Предмет: Русский язык,
автор: ktoto6050
Предмет: Математика,
автор: xxlalenaxxl
Предмет: Геометрия,
автор: yuliuapolyakov