Предмет: Алгебра,
автор: MaksimStepanenko
50 баллов. срочно!
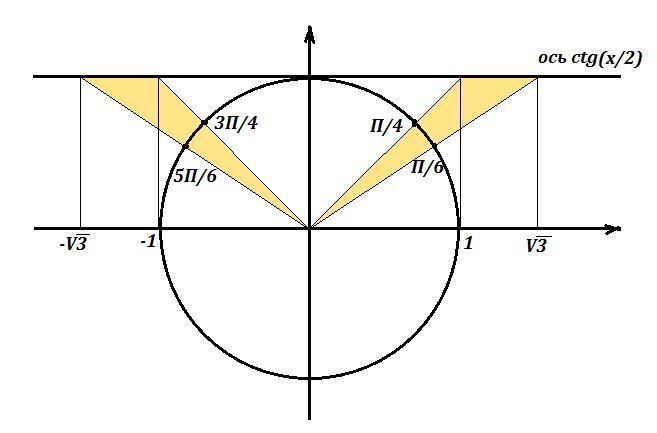
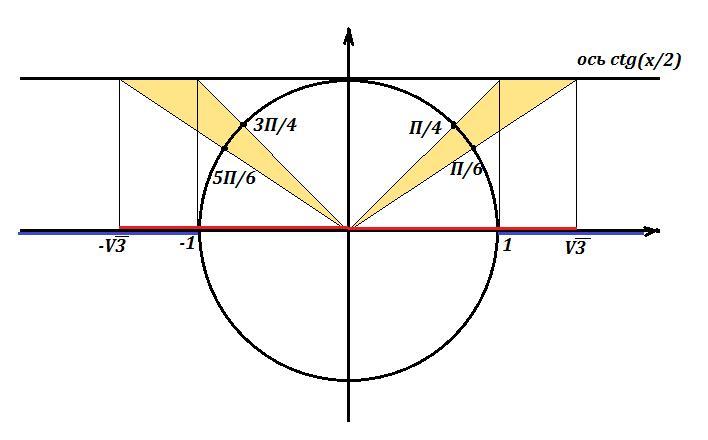
2<2^(sinx/1-cosx)^2<8
Ответы
Автор ответа:
2
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: shuvalovavara
Предмет: История,
автор: mariavigovska0
Предмет: МХК,
автор: olesia0073
Предмет: Геометрия,
автор: rinabumchik