Исследовать функции на монотонность и экстремулы.
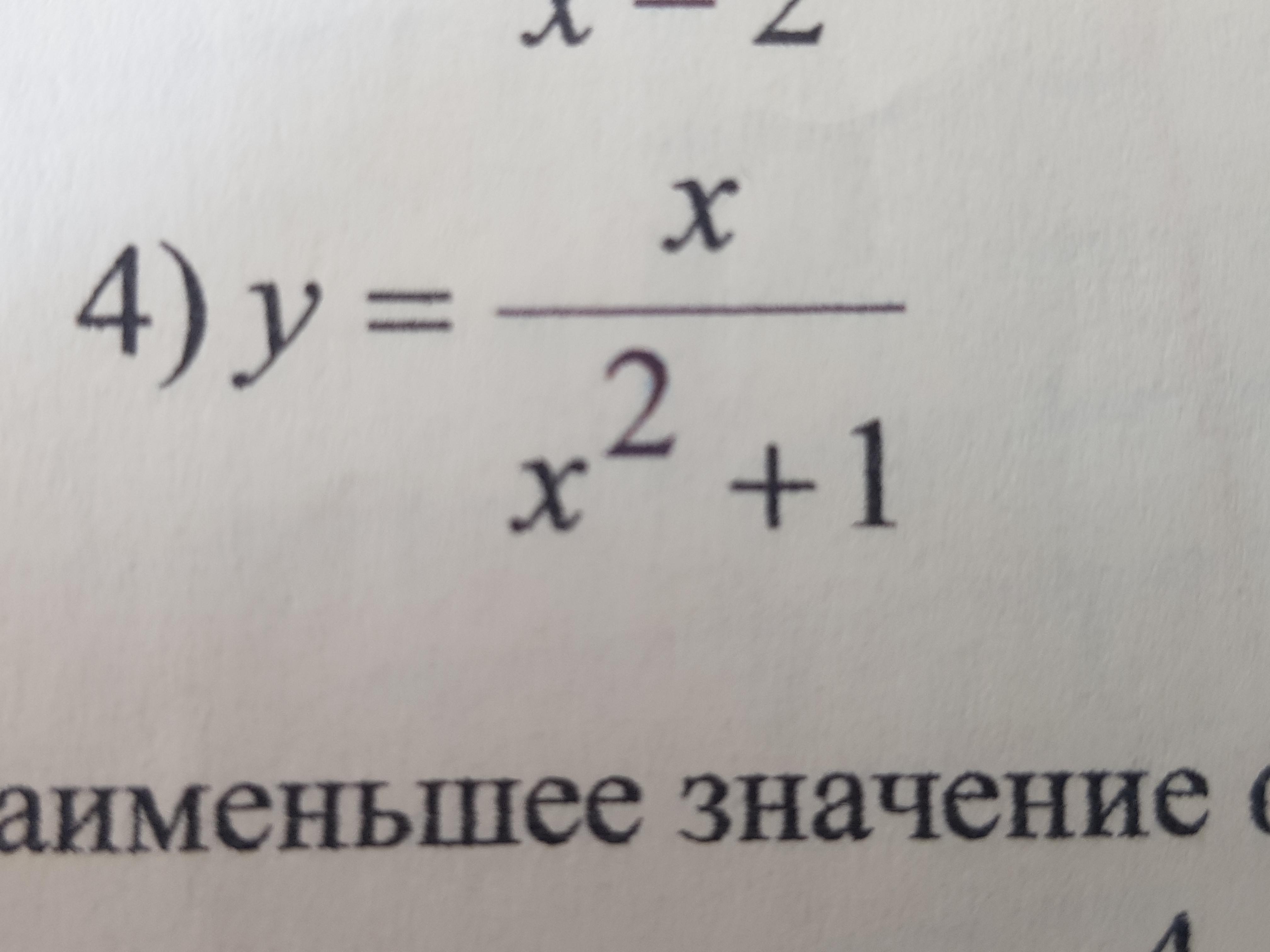
Ответы
ДАНО: y(x) = x/(x²+1)
ИССЛЕДОВАНИЕ (полное - не нужное - исключить).
1. Область определения функции.
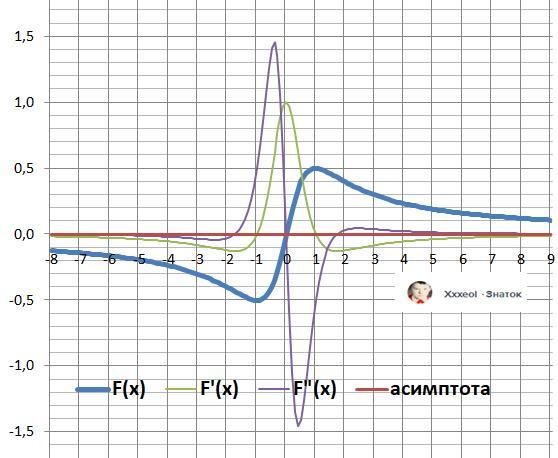
D(y) = R = (-∞;+∞) - непрерывная.
2. Вертикальных асимптот - нет - нет разрывов.
3. Периодичность - нет - не тригонометрическая.
4. Пересечение с осями координат.
С осью ОХ: Y=0 при Х = 0 - нуль функции.
С осью ОУ: y(0) = 0.
5. Интервалы знакопостоянства.
Отрицательна: y(x)<0: X∈(-∞;0). Положительна: y(x)≥0: X∈[0;+∞).
6. Проверка на чётность.
y(-x) = - y(x) - функция нечётная.
7. Первая производная - поиск экстремумов.
y'(x) = -2*x²/(x²+)² - 1/(x²+1) = (1 - x²)/(x²+1)² = 0
В числителе: 1-x² = (1 - x)*(1 + x) = 0
x1 = - 1, x2 = 1 - точки экстремумов.
8. Локальные экстремумы.
Минимум: y(-1) = -0.5, максимум: y(1) = 0.5.
9. Интервалы монотонности.
Производная отрицательная - функция убывает. Функция непрерывная - квадратные скобки на границах.
Убывает: X∈(-∞;-1]∪[1;+∞), возрастает: X∈[-1;1].
10. Вторая производная - поиск точек перегиба.
y"(x) = - 4*x*(1-x²)/(x²+1)³ - 2*x/(x²+1)² = 2*x*(x²-3)/(x²+1)³ = 0
x² - 3 = 0, x1 = 0, x2 = -√3, x3 = √3 - точки перегиба.
11. Поведение функции.
Выпуклая - "горка" - X∈(-∞;-√3]∪[0;√3].
Вогнутая - "ложка" - X∈[-√3;0]∪[√3;+∞)
12. Наклонная асимптота: y = k*x+b.
k = lim(∞) Y(x)/x = 0.
b = lim(∞)Y(x) - k*x = 0
Горизонтальная асимптота: y = 0.
13. Рисунок с графиками исследования - в приложении.