Question

ПОМОГИТЕ!!! СРОЧНОООО

Answer 1

$1)\; \; y=-3x^2+6x-2$

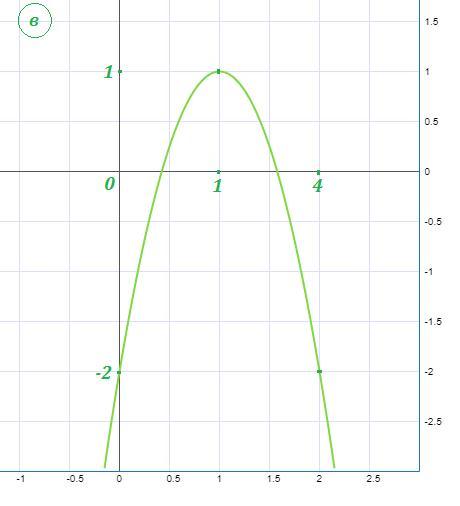
а)  координаты вершины  (1,1) :  $x=-\frac{b}{2a}=-\frac{6}{-6}=1$  ,

$y(1)=-3\cdot 1^2+6\cdot 1-2=1$  .

б)  ветви направлены вниз, т.к.  а= -3<0 .

в) при построении графика легко найти точку пересечения с осью ОУ:   $y(0)=-3\cdot 0^2+6\cdot 0-2=-2$  .Также легко найти симметричную точку для (0,-2) - это точка (4,-2).

г)  точки пересечения с осью ОХ:

 $-3x^2+6x-2=0\; \; \to \\\\3x^2-6x+2=0\; \; ,\; \; D=12\; ,\\\\x_{1,2}=\frac{6\pm \sqrt{12}}{6}=\frac{3\pm \sqrt3}{3}=1\pm \frac{\sqrt3}{3}\\\\x_1=1-\frac{\sqrt3}{3}\; \; ,\; \; x_2=1+\frac{\sqrt3}{3}$

2)  Наибольшее значение функции  $y=-3x^2+6x-2$  будет достигаться в её вершине, а это у(1)=1 .

Answer 2

1б. Если а>0 то ветви параболы направленны вверх, а<0 то ветви параболы направлены вниз. В нашем случае ветви смотрят вниз

1г. Корни уравнения являются точками пересечения

2. Если ветви параболы направлены вниз(наш случай), то наибольшее значение достигается в его вершине (высшая точка функции)

Попытка №2 x)