Предмет: Математика,
автор: renhen723406
Очень очень надо помогите пожалуйста
Садовником осенью было посажено семь саженцев яблони. Вероятность того, что любой из саженцев весной прорастут, в среднем составляет 0,7. Вычислить вероятность того, что из семи саженцев яблони весной прорастут: 1) три саженцы; 2) не менее трех. Найти вероятнее всего число саженцев, которые весной прорастут, и вычислить соответствующую вероятность.
Ответы
Автор ответа:
0
Пошаговое объяснение:
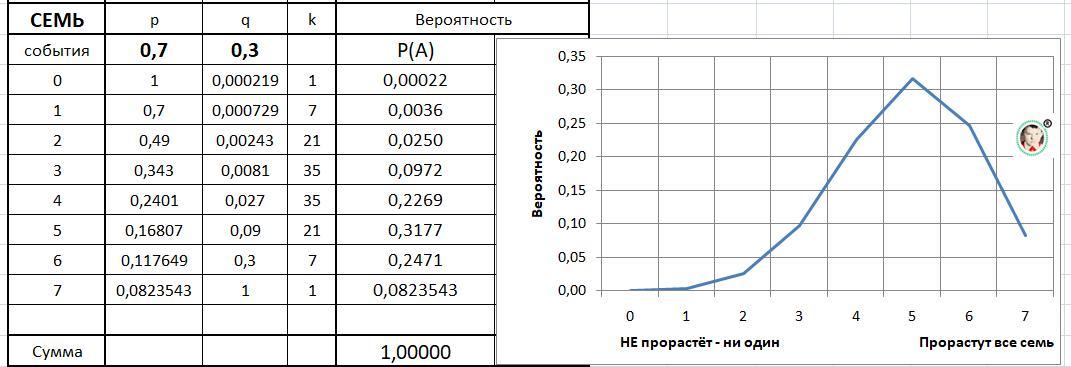
Расчет сведен в таблицу, По данным построен график функции вероятности и всё это в приложении.
Вероятность - прорастут - р = 0,7 - дано.
Вероятность - замерзнут - q = 1 - p = 0.3
Для семи испытаний записываем формулу полной вероятности:
(p+q)⁷ = p⁷ + 7*p⁶*q + ....... + 7*p*q⁶ + q⁷ = 1.
Коэффициенты разложения находим из треугольника Паскаля (рисунков в приложении).
Переходим к решению задачи.
1) Взойдут только три - это Р(3) = 21*0,7³*0,3⁴ = 0,0972 - ответ.
2) Не менее трёх - это один ИЛИ два ИЛИ три. Вероятность событий ИЛИ равна сумме вероятностей каждого
Р(≤3) = 0,0036 + 0,0250+ 0,0972 = 0,1258 - ответ
3) Наиболее вероятное число, по таблице или графику - 5 шт. с вероятностью 0,3177 - ответ.
Приложения:

Похожие вопросы
Предмет: Математика,
автор: NinjaArtem
Предмет: Биология,
автор: Vovikdorik
Предмет: Английский язык,
автор: ZuevYaroslav
Предмет: История,
автор: kotenek1985
Предмет: Биология,
автор: N0Name322