Question

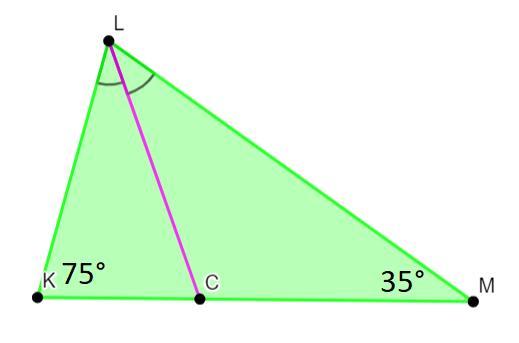
В треугольнике KLM проведена биссектриса LC, K=75°, M=35°
a)Докажите, что треуг LCM равнобедренный.
б) Сравнте отрезки LM и LC.
И желательно начертите треугольник с биссектриссой, и всем остальным

Answer 1

а)

• Сумма углов треугольника равна 180°.

В △KLM:

∠K+∠L+∠M = 180°;

∠L = 180°-(∠K+∠M);

∠L = 180°-(75°+35°);

∠L = 180°-110° = 70°.

∠CLM = ∠KLM:2 = 70°:2 = 35°, как угол при биссектрисе LC ∠KLM.

Рассмотрим △LCM:

∠CLM = 35° = ∠CML;

△LCM - равнобедренный т.к. два его угла равны между собой, что и требовалось доказать.

б)

• Сумма углов треугольника равна 180°.

В △LCM:

∠L+∠C+∠M = 180°;

∠C = 180°-(∠L+∠M);

∠C = 180°-(35°+35°);

∠C = 180°-70° = 110°;

• В треугольнике напротив большего угла лежит большая сторона.

∠С = 110°, напротив сторона LM;

∠M = 35°, напротив сторона LC;

∠C > ∠M  ⇒  LM > LC.

Ответ: LM > LC.