Предмет: Алгебра,
автор: KoralinaJ
Как решить ОДЗ? Объясните, плес)
Приложения:
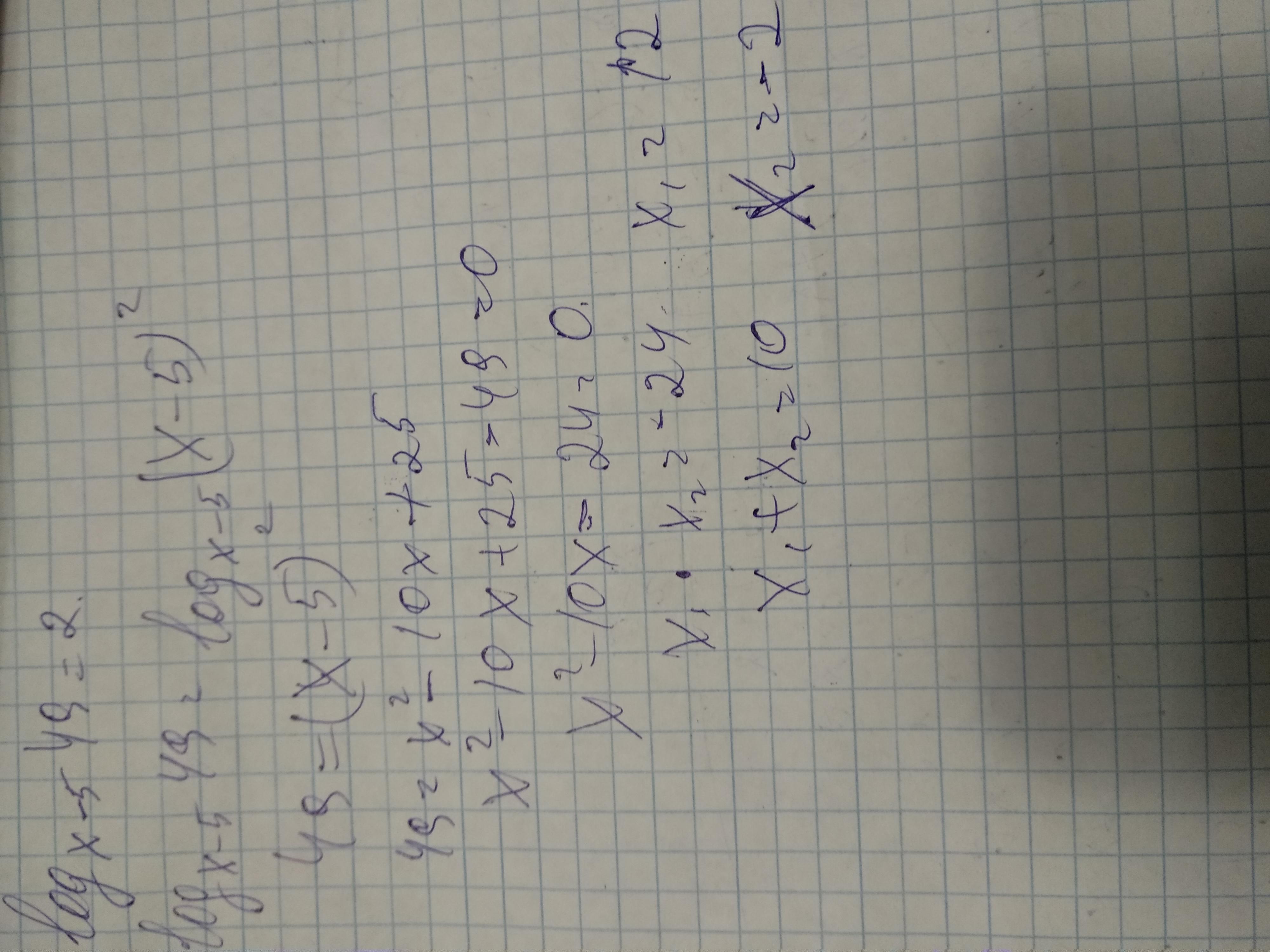
NNNLLL54:
ОДЗ: основание log должно быть >0 и не 1, а агумент >0, то есть {x-5>0, x-5 не=1 , (x-5)^2>0} --> {x>5, x не= 6, x-5 не=0} --> {x>5 , х не=6}
Ответы
Автор ответа:
0
ОДЗ: основание log должно быть >0 и не 1, а агумент >0, то есть
Откуда 6?
Похожие вопросы
Предмет: Физика,
автор: gffihfyfhc
Предмет: Алгебра,
автор: tyupum34
Предмет: Қазақ тiлi,
автор: turashgulzira080
Предмет: Математика,
автор: Vika7016
Предмет: Физика,
автор: Аноним