Предмет: Алгебра,
автор: хочуха04
помогите сделать задание 15.8
Приложения:
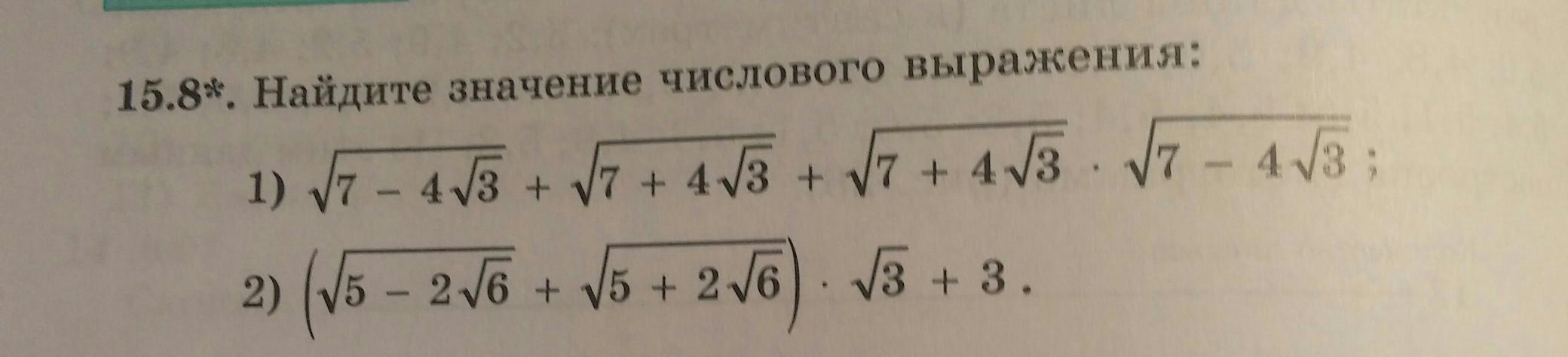
Ответы
Автор ответа:
0
Объяснение:
- Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
- Для любых действительных чисел a и b таких, что a ≥0 и b≥0 выполняется равенство
1.
2.
Также использовали формулы:
Приложения:
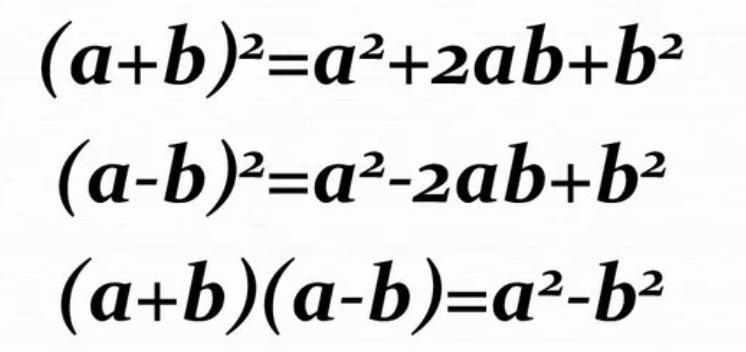
Похожие вопросы
Предмет: Математика,
автор: jamilakanybek1710
Предмет: География,
автор: ershovk8888
Предмет: Химия,
автор: OlivkaTop
Предмет: Алгебра,
автор: Dema133722
Предмет: Математика,
автор: Барашек2004