Предмет: Алгебра,
автор: asgeras28
Помогите решить уравнение
{x/y+y/x=5,2
{x^2-y^2=24
Приложения:
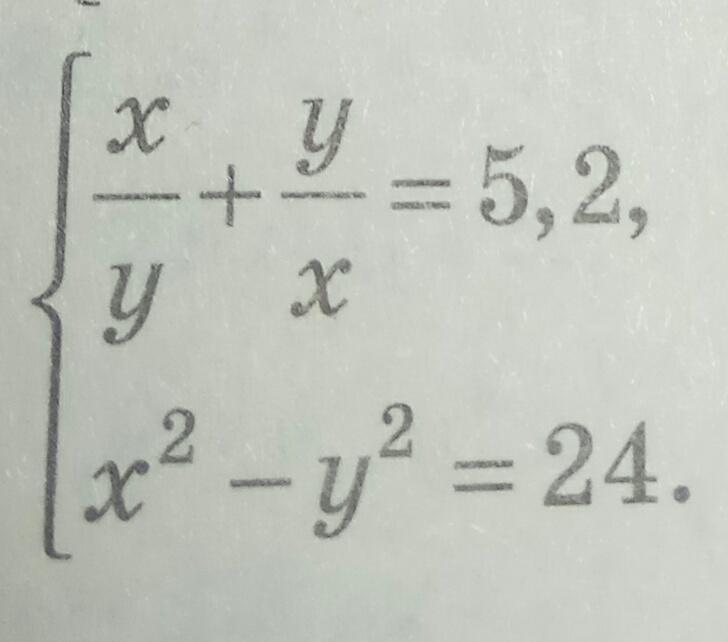
Ответы
Автор ответа:
2
Преобразуем первое уравнение, сделав замену :
Решений нет
Ответ : (5 ; 1) , (- 5 ; - 1)
Похожие вопросы
Предмет: Математика,
автор: MelanieQWq
Предмет: Информатика,
автор: KirillBabkak
Предмет: Английский язык,
автор: vova33944
Предмет: Обществознание,
автор: Dr24
Предмет: Геометрия,
автор: Roza006